Признак сравнения
Даны два ряда с положительными членами
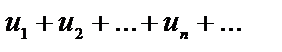 (1),
(1),
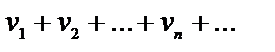 (2),
(2),
причем известно, что члены ряда (1) не превосходят соответствующих членов ряда (2), т.е. 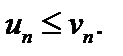
Из сходимости ряда (2) следует сходимость ряда (1). Из расходимости ряда (1) следует расходимость ряда (2).
Пример 1. Ряд 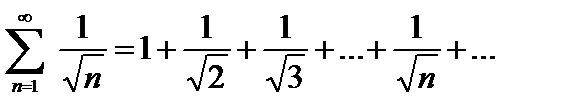
с общим членом 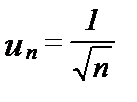
сравним с гармоническим расходящимся рядом 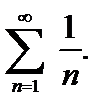
Его общий член 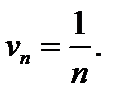
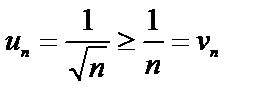 (u1=v1; u2>v2; u3>v3; …)
(u1=v1; u2>v2; u3>v3; …)
По признаку сравнения ряд 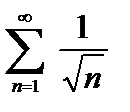 расходится.
расходится.
Пример 2. Ряд 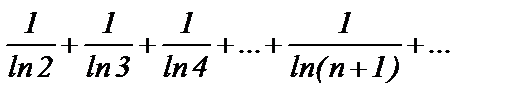 с общим членом
с общим членом 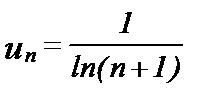 сравним с рядом
сравним с рядом 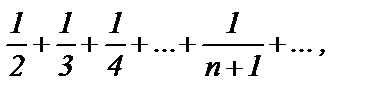 общий член которого
общий член которого 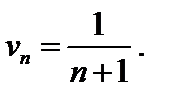
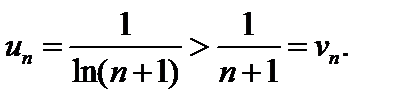
Ряд 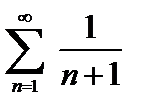 является остатком гармонического ряда и расходится.
является остатком гармонического ряда и расходится.
По признаку сравнения расходится ряд 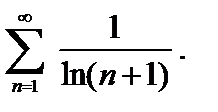
Пример 3. Ряд 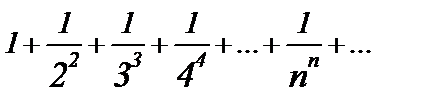 сходится, т. к. его члены не превосходят соответствующих членов ряда
сходится, т. к. его члены не превосходят соответствующих членов ряда 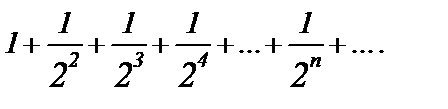 Но последний ряд сходится как ряд геометрической прогрессии со знаменателем
Но последний ряд сходится как ряд геометрической прогрессии со знаменателем 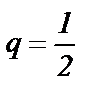 , точнее
, точнее 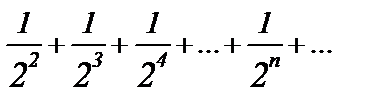 – ряд геометрической прогрессии с первым членом
– ряд геометрической прогрессии с первым членом 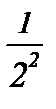 и
и 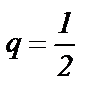 . Его сумма
. Его сумма 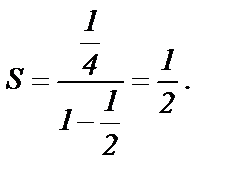 Тогда сумма ряда
Тогда сумма ряда 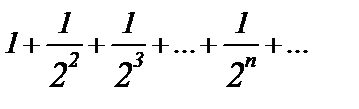 равна
равна 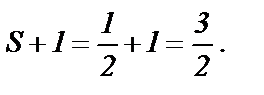
Пример 4. Сравним ряд 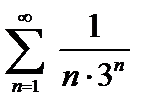 с рядом геометрической прогрессии
с рядом геометрической прогрессии 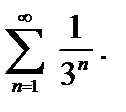 Легко видеть, что оба ряда сходятся.
Легко видеть, что оба ряда сходятся.
Признак Даламбера. Если для ряда с положительными членами 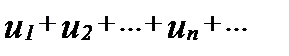 существует конечный предел
существует конечный предел 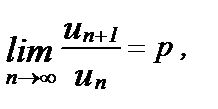 то при р<1 ряд сходится, при p>1 ряд расходится.
то при р<1 ряд сходится, при p>1 ряд расходится.
Заметим, что при p=1 признак не дает ответа на вопрос о сходимости ряда.
Пример 5. Исследовать сходимость ряда
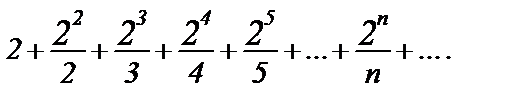
Общий член ряда 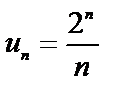 . Следующий за ним член ряда
. Следующий за ним член ряда 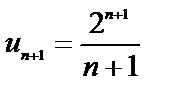 Найдем
Найдем 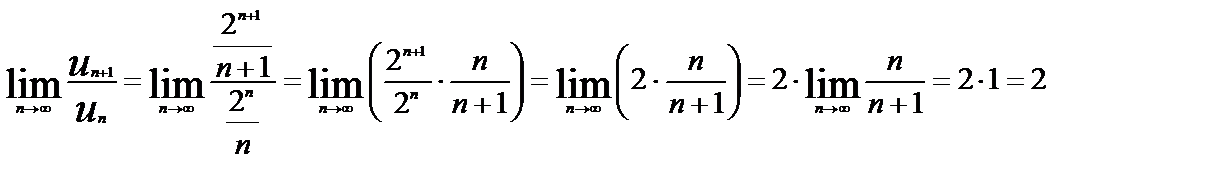 т. к. полученный предел 2>1, то ряд расходится.
т. к. полученный предел 2>1, то ряд расходится.
Заметим, что для вычисления 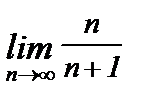 следует разделить числитель и знаменатель на n и учесть, что
следует разделить числитель и знаменатель на n и учесть, что 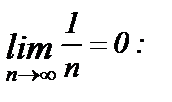
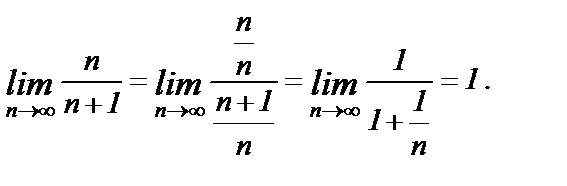
Пример 6. Исследовать сходимость ряда 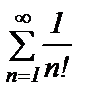 .
.
Здесь символ n! (читают: эн факториал) обозначает произведение n натуральных чисел от 1 до n, т. е. 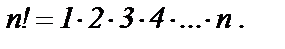
Так 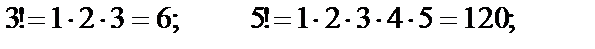
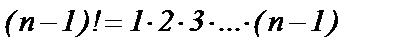
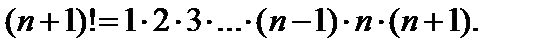
Вернемся к данному ряду
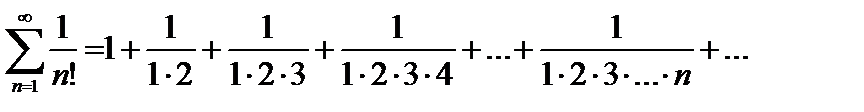
Здесь 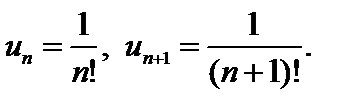
Вычислим 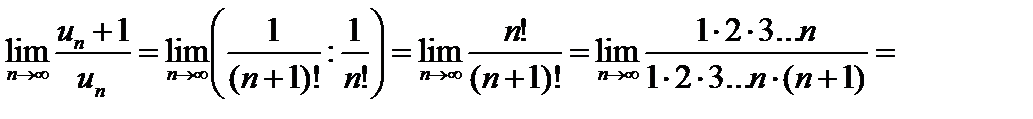
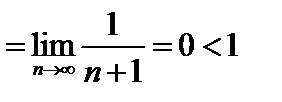
Т.к. полученный предел 0<1, то ряд сходится.
Пример 7. Исследовать сходимость ряда 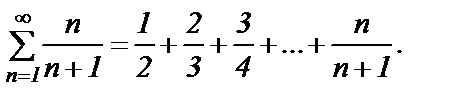
Здесь 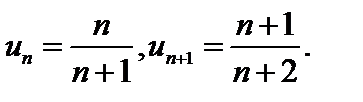
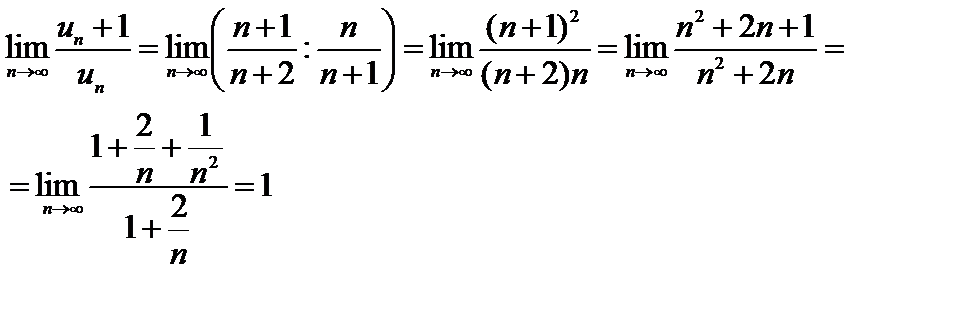
Для вычисления предела числитель 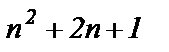 и знаменатель
и знаменатель 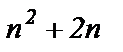 следует разделить на
следует разделить на 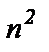 и учесть, что при
и учесть, что при 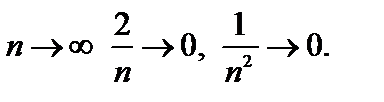
Т.к. полученный предел равен 1, то признак Даламбера вопроса о сходимости ряда не решает.
Применим признак сравнения и сравним ряд 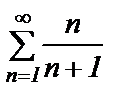 с рядом
с рядом 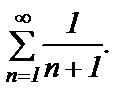
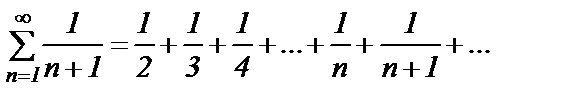 — гармонический ряд без первого члена (остаток гармонического расходящегося ряда). Итак, ряд
— гармонический ряд без первого члена (остаток гармонического расходящегося ряда). Итак, ряд 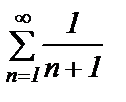 расходится, а т.к.
расходится, а т.к. 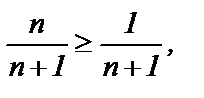 то и данный ряд расходится.
то и данный ряд расходится.
Дата добавления: 2014-12-30; просмотров: 1308;
