Предел последовательности
В основе математического анализа лежит понятие предела переменной величины, с помощью которого определяются другие понятия: непрерывность функции, производная, определенный интеграл и т.д.
Рассмотрим определение предела последовательности и некоторые способы отыскания предела последовательности. Для начала обратимся к примерам.
Последовательность 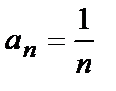 имеет вид
имеет вид 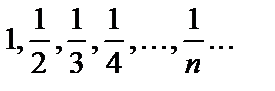 .
.
Ясно, что величина членов этой последовательности с ростом номера n неограниченно уменьшается, приближаясь к нулю.
Последовательность 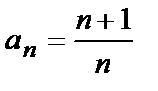 имеет вид
имеет вид 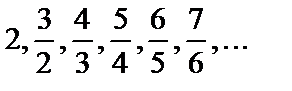 .
.
Ясно, что с ростом номера n величина членов последовательности приближается к единице, т.е. члены последовательности отличаются от единицы тем меньше, чем больше номер n.
Последовательность 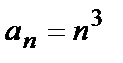 имеет вид 1,8,27,64,125, ... .
имеет вид 1,8,27,64,125, ... .
Ясно, что величина членов этой последовательности неограниченно увеличивается.
Последовательность 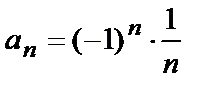 имеет вид
имеет вид 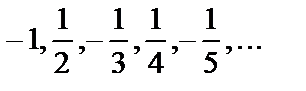 .
.
В отличие от рассмотренного уже примера 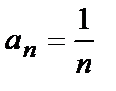 члены этой последовательности
члены этой последовательности 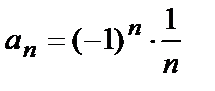 имеют разные знаки, но абсолютная величина их членов с ростом номера n неограниченно уменьшается, приближаясь к нулю. Какое бы (даже очень малое) положительное число мы не задали (например
имеют разные знаки, но абсолютная величина их членов с ростом номера n неограниченно уменьшается, приближаясь к нулю. Какое бы (даже очень малое) положительное число мы не задали (например 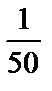 ), понятно, что, начиная с номера n=50, все последующие члены последовательности
), понятно, что, начиная с номера n=50, все последующие члены последовательности 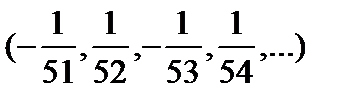 по абсолютной величине будут меньше выбранного числа
по абсолютной величине будут меньше выбранного числа 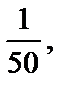 т.е. для всех n > 50
т.е. для всех n > 50 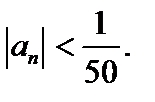
Такие последовательности называют бесконечно малыми, их предел равен нулю и факт этот записывают так:
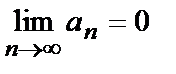
(Читают: предел 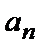 при n стремящемся к бесконечности равен нулю).
при n стремящемся к бесконечности равен нулю).
Для последовательности 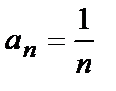 аналогично
аналогично 
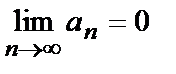 или
или 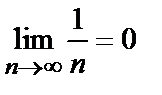 .
.
Для последовательности 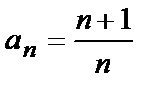 запишем
запишем 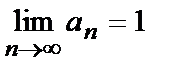 или
или 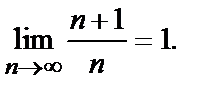
Что касается последовательности an=n3, то величина ее членов увеличивается неограниченно. Такие последовательности называют бесконечно большими, они не имеют предела и факт этот записывают так:

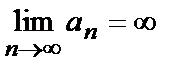 или
или 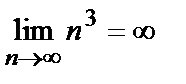 .
.
(Читают: предел an равен бесконечности).
Здесь знак ¥ (бесконечность) означает только то, что последовательность неограниченно возрастает и не имеет предела.
Дадим точное определение предела последовательности.
Определение. Число А называется пределом последовательности а1,а2,...,аn,..., если для любого положительного числа 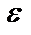 существует такой номер
существует такой номер 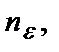 что для всех n>
что для всех n> 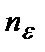 выполняется неравенство
выполняется неравенство 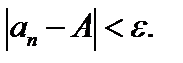
Этот факт записывают так:
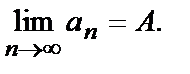
(Читают: предел последовательности 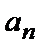 при n стремящемся к бесконечности равен А).
при n стремящемся к бесконечности равен А).
Иногда пользуются записью: 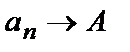 при n®¥×
при n®¥×
Заметим, что в определении предела используют число 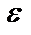 (эпсилон). Это положительное, сколь угодно малое число. Число А может быть для различных последовательностей любым действительным числом.
(эпсилон). Это положительное, сколь угодно малое число. Число А может быть для различных последовательностей любым действительным числом.
В рассмотренных примерах: А=0.
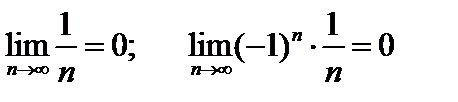
А=1 для последовательности 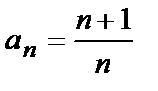 или
или 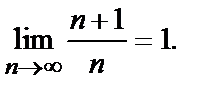
Рассмотрим последовательность 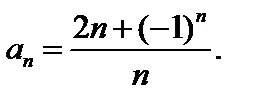 Ее члены имеют вид
Ее члены имеют вид 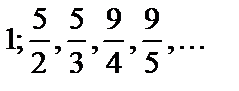 . Покажем, что
. Покажем, что 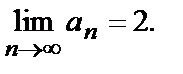 Для этого преобразуем
Для этого преобразуем 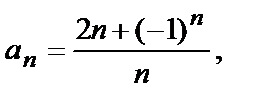 разделив числитель почленно на знаменатель:
разделив числитель почленно на знаменатель: 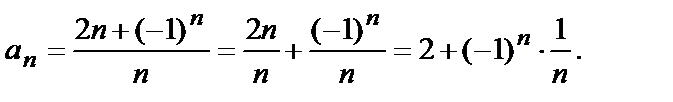
Та же последовательность запишется несколько иначе:
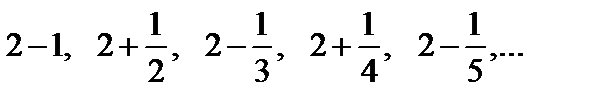 .
.
Теперь видно, что с ростом номера n члены последовательности отличаются от числа 2 все меньше и меньше. Для любого положительного числа e (например,e = 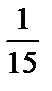 ) можно найти номер (ne=15) ne такой, что для всех номеров n>ne (n>15) выполняется неравенство
) можно найти номер (ne=15) ne такой, что для всех номеров n>ne (n>15) выполняется неравенство 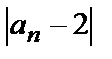 <e.
<e.
А именно: 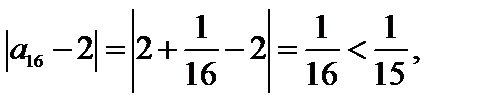
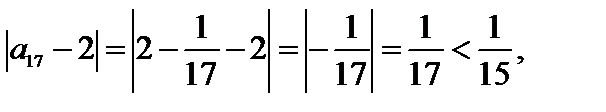
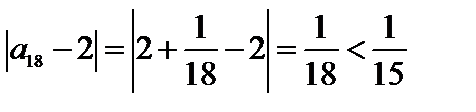 и т.д.
и т.д.
Заметим, что не всякая последовательность обязательно имеет предел.
Рассмотрим последовательность
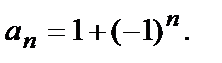
Ее члены: 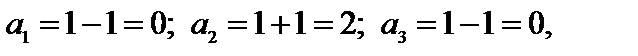 т.е. последовательность представляет собой 0,2,0,2,0,2,... .
т.е. последовательность представляет собой 0,2,0,2,0,2,... .
Ясно, что члены этой последовательности остаются равными либо 0, либо 2 и не приближаются ни к какому пределу, т.е. 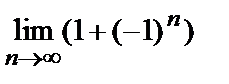 не существует.
не существует.
Вспомним уже знакомые из курса средней школы последовательности: арифметическую и геометрическую.
Арифметическая последовательность 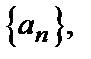 где
где 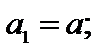
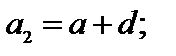
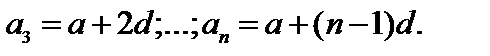
Сумма первых n членов арифметической прогрессии 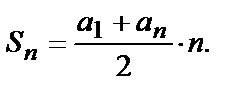
Геометрическая последовательность 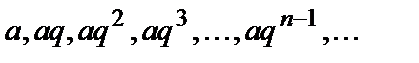
Сумма первых n членов геометрической прогрессии 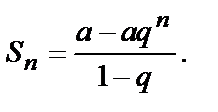
Дата добавления: 2014-12-30; просмотров: 1297;
