Определение.

Два множества А и В называются равными, если каждый элемент множества А является элементом множества В, и наоборот, каждый элемент множества В является элементом множества А.

Пусть А={-1;0;1}; В - множество корней уравнения

х³-х=0.

Так как корни уравнения х(х-1)(х+1)=0 есть числа 0;1;-1, то множество В={0;1;-1}. Отсюда А=В.

Заметим, что порядок, в каком записаны элементы множества, для множества не существенен.

Рассмотрим числовые множества.

Натуральное число является основой всей математики. Это абстрактное понятие возникло из необходимости вести счет предметам различной природы, входящим в то или иное множество.

Понятие числа формировалось еще в глубокой древности, так как оно было необходимо для всевозможных подсчетов, для измерения земельных участков, для ведения счета времени и решения многих других вопросов.

Обычно натуральные числа записывают в виде 1,2,3,4,..., но они могут быть представлены также многими другими способами. Римляне их записывали знаками: I, II, III, IY, ...; для электронных вычислительных машин оказалось самой удобной двоичная система счисления, куда входят лишь символы 0 и 1.

В первобытном обществе человек нуждался лишь в нескольких первых числах, но с развитием общества ему понадобились все большие и большие числа. Еще в Древней Греции до Архимеда не умели записывать большие числа. В III веке до н. э. Архимед, замечательный математик, физик, механик построил научную систему счисления, давшую возможность выражать как угодно большие числа.

Скачок от конечного к бесконечному совершили греческие математики, впервые приступившие к изучению натурального ряда чисел. Смелая идея бесконечности открыла для математики огромные возможности.

Операции над числами привели к расширению понятия числа. Если действия сложения и умножения двух натуральных чисел дают вновь натуральные числа, то действия вычитания и деления не всегда возможны на множестве натуральных чисел. Возникает необходимость рассмотрения множества целых чисел

Z={...,-n,...,-4,-3,-2,-1,0,1,2,3,4,...,n,...}

и множества рациональных чисел. В Древней Греции не было отрицательных чисел. Честь их открытия приписывается индусам. В Европе отрицательные числа вошли в употребление в эпоху Возрождения.

Изучение дробей было предпринято уже в Древнем Египте (около 2000 г. до н. э.). В Древнем Вавилоне были созданы многие единообразные правила арифметических действий с дробями.

В виде дроби 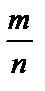всегда можно записать и целое число. Например,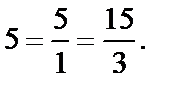

Числа, имеющие вид 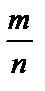, где m и n - целые числа, называются рациональными, а множество всех рациональных чисел обычно обозначают буквой Q.

В Древней Греции было установлено, что потребности геометрии не обеспечиваются рациональными числами. На основании теоремы Пифагора квадрат длины гипотенузы прямоугольного треугольника с катетами, равными единице, равен двум: 1²+1²=2.

Было доказано, что не существует рационального числа, квадрат которого равен двум. Чтобы выразить длину каждого отрезка каким-либо числом, в математику были введены иррациональные числа ( 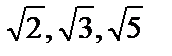и другие), каждое из которых не может быть равно рациональному числу и только приближенно представляется рациональным числом. Иррациональные числа вместе с рациональными составляют множество действительных чисел (часто обозначается буквой R).

Вы знаете, что множество R действительных чисел может быть изображено точками числовой оси. Любое действительное число изображается точкой числовой оси, расположенной от выбранного начала точки О на расстоянии, равном этому числу. Наоборот, каждая точка оси изображает единственное действительное число, а именно, если точка лежит справа от точки О, то она изображает положительное число, а если – слева, то отрицательное действительное число. Таким образом, устанавливается взаимно-однозначное соответствие между множеством всех действительных чисел и множеством всех точек числовой оси.

Необходимость решения квадратных уравнений привела к введению комплексных чисел. Если уравнение х²-1=0 или х²=1 имеет два корня +1 и -1, то уравнение х²+1=0 на множестве действительных чисел корней не имеет.

В рассмотрение был введен новый символ - мнимая единица i такая, что
i × i = i² = -1. Впервые мнимая единица появилась в XVI в. В связи с решением алгебраических уравнений. В настоящее время комплексные числа широко применяются как в самой математике, так и в ее приложениях.

Многие математические теории приняли законченный совершенный вид благодаря использованию комплексных чисел. Так, в области комплексных чисел всякое алгебраическое уравнение степени n имеет ровно n корней.

Комплексные числа необходимы для описания различных явлений природы. С их помощью решаются уравнения электростатики, аэро- и гидродинамики, теории колебаний, квантовой механики.