Решение. Последовательно интегрируем дважды, применив предварительно формулу:
а) 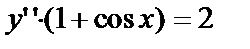 или
или 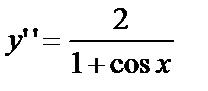 — Д.У.-II
— Д.У.-II
Последовательно интегрируем дважды, применив предварительно формулу:
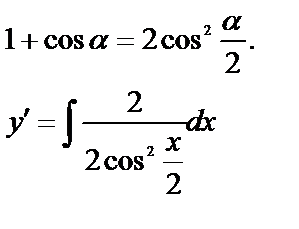
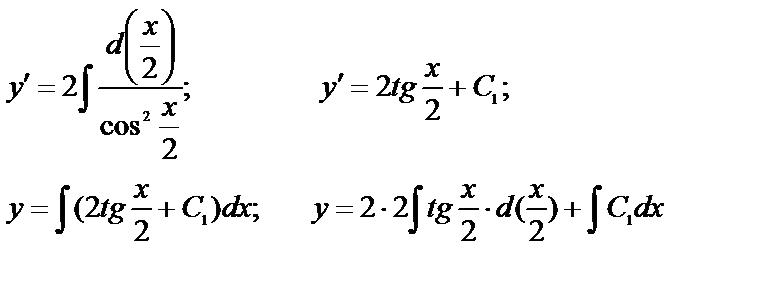
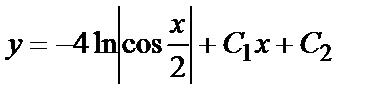 — общее решение.
— общее решение.
б) 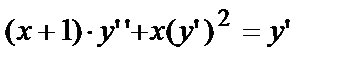 - Д.У.-II, допускающее понижение порядка подстановкой
- Д.У.-II, допускающее понижение порядка подстановкой 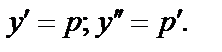
(1) 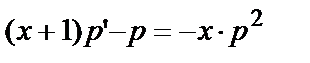 — Д.У.-I типа Бернулли относительно функции
— Д.У.-I типа Бернулли относительно функции 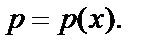 Решаем уравнение (1) подстановкой
Решаем уравнение (1) подстановкой 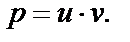
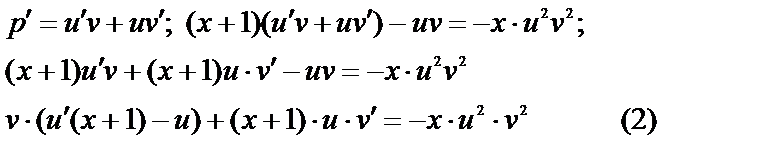
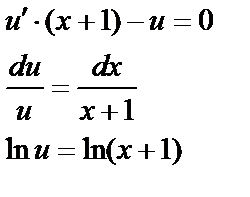
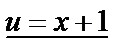 подставим в (2) подставим в (2)
| 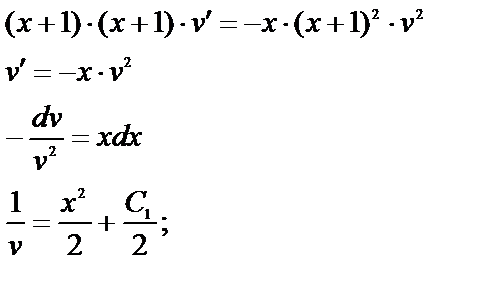
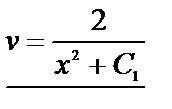
|
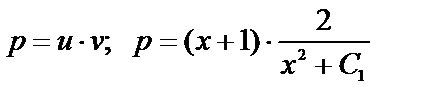 — общее решение уравнения (1).
— общее решение уравнения (1).
Т.к.  то
то 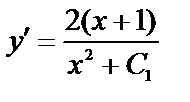 — Д.У.-I (3)
— Д.У.-I (3)
Уравнение (3) с разделяющимися переменными: 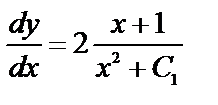 или
или
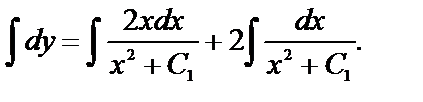
Рассмотрим 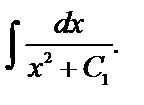
При 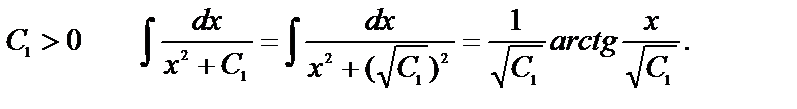
При 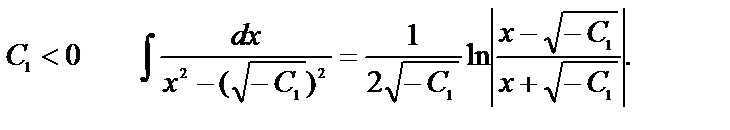
Поэтому общее решение данного уравнения (б)
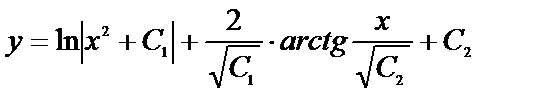

при 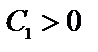
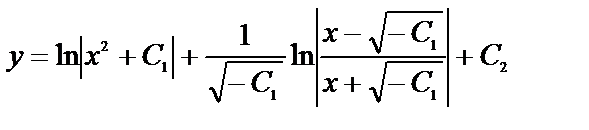 при
при 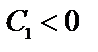
Задача № 5.Найти общее решение уравнения:
а) 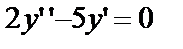
б) 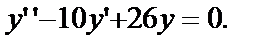
Дата добавления: 2014-12-30; просмотров: 1115;
