Решение. Для того, чтобы решить неравенство на плоскости, надо построить график линии

Для того, чтобы решить неравенство 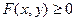на плоскости, надо построить график линии 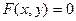. Кривая 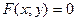разбивает плоскость на части, в каждой из которых выражение 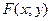сохраняет свой знак. Выбирая пробную точку в каждой из этих частей, найдем часть плоскости, являющуюся искомым решением неравенства.

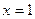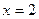1) Построим прямые и , заштрихуем область, в которой 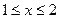. Затем построим параболу 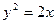и заштрихуем область, содержащую ось симметрии параболы (расположенную внутри параболы); построим прямую 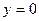и заштрихуем область, лежащую выше прямой. Пересечение всех заштрихованных областей и определит множество точек, представляющих решение рассматриваемой системы.

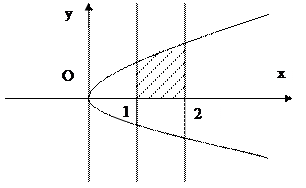
Рис. 18

2) Построим линию, определяемую уравнением 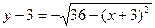. Эта линия представляет собой ту часть окружност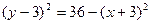и или 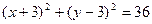, на которой 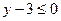. Далее построим прямую 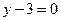( 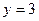). Решением рассматриваемого двойного неравенства является часть плоскости, расположенная между нижней половиной окружности 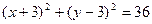с центром в точке 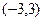радиуса 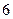прямой .

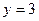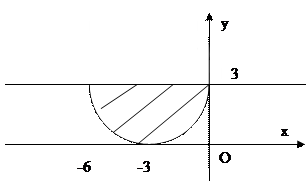
Рис. 19