Решение. Для приведения уравнения кривой второго порядка к каноническому виду применяют метод выделения полного квадрата.
Для приведения уравнения кривой второго порядка к каноническому виду применяют метод выделения полного квадрата.
Сгруппируем слагаемые, содержащие текущие координаты. Коэффициенты при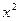 
и 
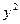вынесем за скобки: 
.
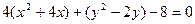Выделим полный квадрат: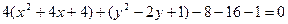 
. Отсюда 
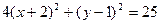. Разделим обе части равенства на 25: 
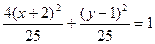. Запишем полученное уравнение в каноническом виде: 
.
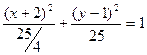Выполним параллельный перенос осей координат по формулам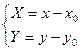 
. При таком преобразовании начало координат переносится в точку 
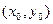, уравнение эллипса принимает канонический вид 
.
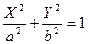В нашем примере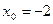 
, 
, 
, 
.
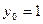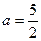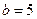Итак, рассматриваемое уравнение определяет эллипс с центром в точке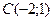 
и полуосям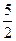и 
и 
.
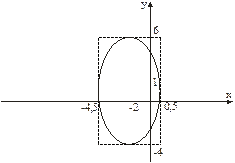
Рис. 13
Пример 2. Привести уравнение кривой второго порядка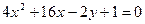 
к каноническому виду и построить кривую.
Дата добавления: 2014-12-07; просмотров: 1232;