Решение. Сначала построим таблицу значений и :
Сначала построим таблицу значений 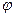 и
и 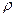 :
:
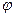
| 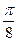
| 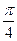
| 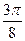
| 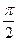
| 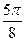
| 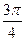
| 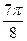
| 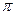
| 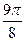
| 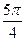
| 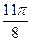
| 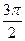
| 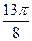
| 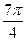
| 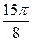
| |
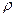
| 2,00 | 1,92 | 1,71 | 1,38 | 1,00 | 0,62 | 0,29 | 0,08 | 0,00 | 0,08 | 0,29 | 0,62 | 1,00 | 1,38 | 1,71 | 1,92 |
Построим эти точки в полярной системе координат. Полярная система координат состоит из начала координат 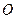 (полюса) и полярной оси
(полюса) и полярной оси 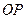 . Координаты точки
. Координаты точки 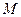 в полярной системе координат определяются расстоянием
в полярной системе координат определяются расстоянием 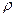 от полюса (полярным радиусом) и углом
от полюса (полярным радиусом) и углом 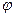 между направлением полярной оси и полярным радиусом (полярным углом). Для того, чтобы построить точку
между направлением полярной оси и полярным радиусом (полярным углом). Для того, чтобы построить точку 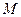 , необходимо построить луч, выходящий из точки
, необходимо построить луч, выходящий из точки 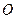 под углом
под углом 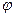 к полярной оси; отложить на этом луче отрезок длиной
к полярной оси; отложить на этом луче отрезок длиной 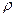 .
.
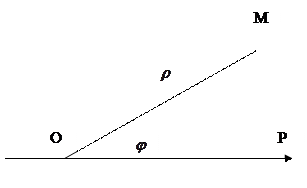
Рис. 15
Построим все точки, определенные в таблице и соединим их плавной линией
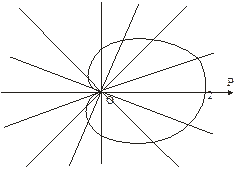
Рис. 16
Запишем уравнение рассматриваемой кривой в прямоугольной декартовой системе координат. Для этого воспользуемся формулами перехода от декартовой к полярной системе координат.
Если полюс совпадает с началом координат прямоугольной декартовой системы координат, полярная ось – с осью абсцисс, то между прямоугольными декартовыми координатами 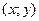 и полярными координатами
и полярными координатами 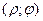 существует следующая связь:
существует следующая связь:
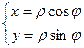 ,
, 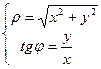
Откуда
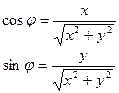
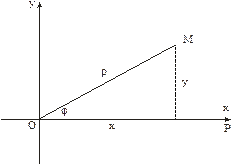
Рис. 17
Итак, в уравнении исходной кривой 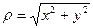 ,
, 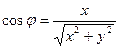 . Поэтому уравнение
. Поэтому уравнение 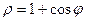 принимает вид
принимает вид 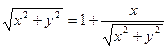 . После преобразований получим уравнение
. После преобразований получим уравнение 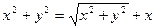 .
.
Дата добавления: 2014-12-07; просмотров: 1435;
