Последовательность. Способы задания

Математический анализ изучает два вида переменной величины: последовательность и функцию непрерывного аргумента. С помощью последовательностей математика изучает дискретные величины. Поскольку любые данные опыта по существу имеют дикретный характер, ясно видна большая роль аппарата последовательностей в математическом отображении действительности.

Последовательность {a_n} - это бесконечный ряд чисел

а₁, а₂, а₃, ..., а_{n ... ,}

заданный с помощью некоторого закона.

Последовательность - функция, у которой аргумент n принимает целые положительные значения 1,2,3,... . Поэтому говорят, что последовательность есть функция натурального аргумента..

Последовательность можно задать различными способами.

1. Одной формулой. Подставляя вместо n натуральные числа, находим члены последовательности.

Пример 1.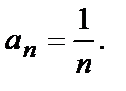

При n=1 a₁=1; при n=2 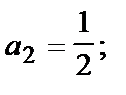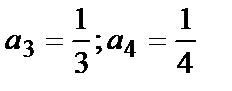и т.д.

Получили последовательность .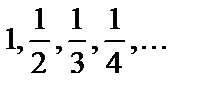

Пример 2.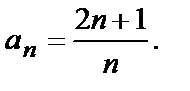

Выпишем несколько ее первых членов, полагая n=1,2,3,4,...

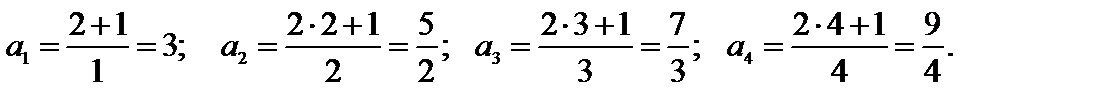
Получили последовательность

.

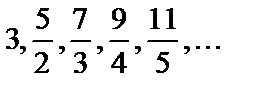Пример 3.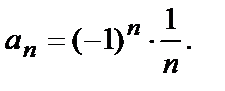

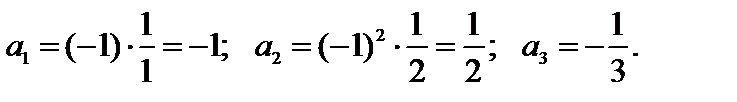
Получили последовательность

.

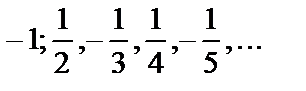2. Зададим последовательность перечислением ее членов:

а₁=0, а₂=1, а₃=0, а₄=1, а₅=0, ..., а_2n=1; а_2n+1=0, …

Получаем последовательность

0, 1, 0, 1, 0, 1, 0, ..., .

закон образования которой ясен, хотя формулу для общего члена а_n мы не записали. Впрочем, для этой последовательности формулу можно записать как

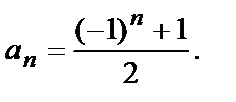
3. Зададим последовательность

0,1,0,1,1,0,1,1,1,0,1,1,1,1,0,... .

(после каждого нуля число единиц увеличивается на одну). Закон образования последовательности ясен, хотя формулу мы не записали.

Итак, формула - это очень употребительный, но не единственный способ задания последовательности.