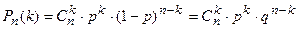I) Биноминальное распределение
Определение._____________________________________________________________________
________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
Вероятность появления события А k раз из общего числа п испытаний можно найти по формуле Бернулли:
|
(11)
где 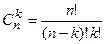 .
.
Ряд распределения случайной величины Х, подчиненной биномиальному закону, можно представить в виде таблицы:
| Х | … | k | … | n | ||
| Р | Cn0· p0·qn | Cn1 ·p1·qn–1 | … | Cnk·pk·qn–k | … | Cnn·pn·q0 |
Пример.На элеваторе работают четыре установки. Вероятность того, что в течение часа любая из них завершит работу равна 0,8. 1) Найти закон распределения случайной величины Х – числа установок, остановившихся в течение часа. Построить функцию распределения. 2) Найти вероятность остановки в течение часа: а) более двух установок; б) от одной до трех установок.
Решение. 1) Возможные значения Х следующие: 0, 1, 2, 3, 4. Вероятность этих значений можно найти по формуле Бернулли, потому что Х имеет биномиальное распределение (станки останавливаются независимо друг от друга с постоянной вероятностью р = 0,8). Получаем:
р4(0)=q4=0,0016,
р4(1)=C41p1q3=0,0256,
р4(2)= C42 p2q2 = 0,154,
р4(3)=C43 · p3· q1=0,41,
р4(4)= p 4 = 0,41.
Закон распределения имеет вид
| Х | |||||
| Р | 0,0016 | 0,0256 | 0,154 | 0,41 | 0,41 |
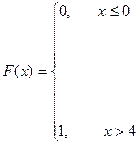
2) а) Р(X>2) = P(X =3)+P(X=4)=0,41+0,41=0,82.
б) P(1≤X≤3)=P(X=1)+P(X=2)+ P(X=3)=0,0256+0,154+0,41=0,59.
Дата добавления: 2014-12-02; просмотров: 1999;