Биномиальное распределение
Пусть производится определенное число n независимых опытов, причем в каждом из них с одной и той же вероятностью может наступить некоторое событие Р. Рассмотрим случайную величину 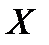 , представляющую собой число наступлений событий A в n опытах. Закон ее распределения имеет вид
, представляющую собой число наступлений событий A в n опытах. Закон ее распределения имеет вид
Значения 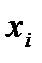
| … | n | |||
Вероятности 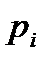
| 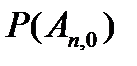
| 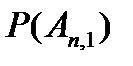
| 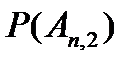
| 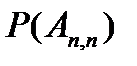
|
Где 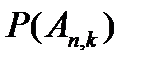 , вычисляется по формуле Бернулли.
, вычисляется по формуле Бернулли.
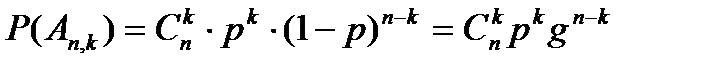
Закон распределения, который характеризуется такой таблицей, называется биноминальным.
Задача. Монету подбрасывают 5 раз. Составить закон распределения случайной величины 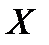 - числа выпадения герба.
- числа выпадения герба.
Решение. Возможны следующие значения случайной величины 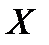 : 0, 1, 2, 3, 4, 5. Зная, что вероятность выпадения герба в одном испытании равна
: 0, 1, 2, 3, 4, 5. Зная, что вероятность выпадения герба в одном испытании равна 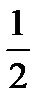 , найдем вероятности значений случайной величины
, найдем вероятности значений случайной величины 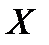 по формуле Бернулли:
по формуле Бернулли:
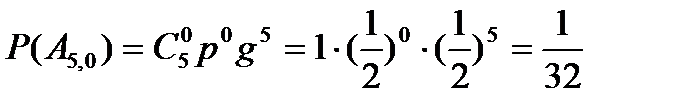 ;
; 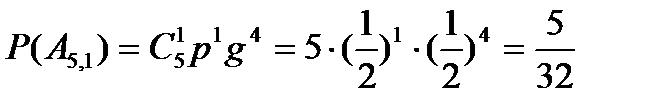 ;
;
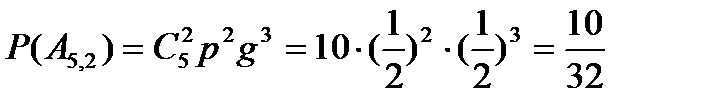 ;
; 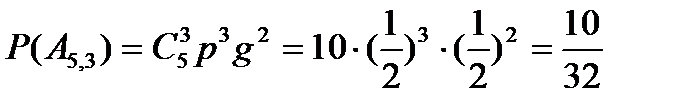 ;
;
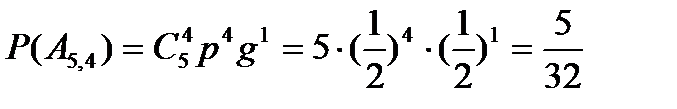 ;
; 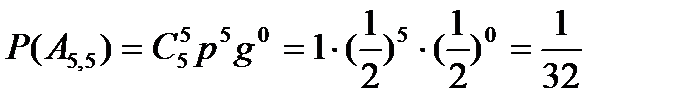 .
.
Закон распределения имеет вид
Значения 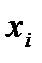
| ||||||
Вероятности 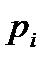
| 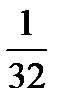
| 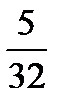
| 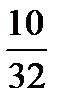
| 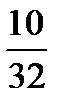
| 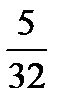
| 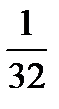
|
Сделаем проверку: 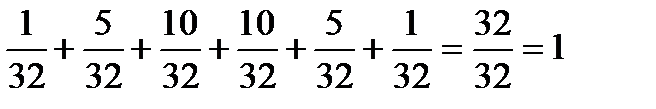 .
.
Дата добавления: 2014-12-05; просмотров: 6101;
