Закон распределения случайной величины
Соотношение, устанавливающее тем или иным способом связь между возможными значениями случайной величины и их вероятностями, называется законом распределения случайной величины.
Закон распределения дискретной случайной величины обычно задается рядом распределения:
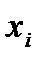
| 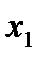
| 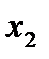
| 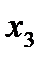
| … | 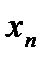
|
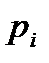
| 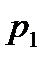
| 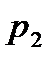
| 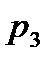
| … | 
|
При этом 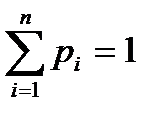 , где суммирование распространяется на все (конечное или бесконечное) множество возможных значений данной случайной величины
, где суммирование распространяется на все (конечное или бесконечное) множество возможных значений данной случайной величины 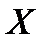 .
.
Задача 1. Даны вероятности значений случайной величины 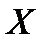 : значение 10 имеет вероятность 0,3; значение 2 – вероятность 0,4; значение 8 – вероятность 0,1; значение 4 – вероятность 0,2. Построить ряд распределения случайной величины
: значение 10 имеет вероятность 0,3; значение 2 – вероятность 0,4; значение 8 – вероятность 0,1; значение 4 – вероятность 0,2. Построить ряд распределения случайной величины 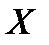 .
.
Решение. Расположив значения случайной величины в возрастающем порядке, получим ряд распределения:
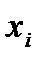
| ||||
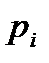
| 0,4 | 0,2 | 0,1 | 0,3 |
Возьмем на плоскости хОр точки (2; 0,4), (4; 0,2), (8; 0,1) и (10; 0,3). Соединив последовательные точки прямолинейными отрезками, получим многоугольник (или полигон) распределения случайной величины 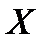
Задача 2. Разыгрываются две вещи стоимостью по 5000 руб и одна вещь стоимостью 30000 руб. Составить закон распределения выигрышей для человека, купившего один билет из 50.
Решение. Искомая случайная величина 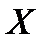 представляет собой выигрыш и может принимать три значения: 0, 5000 и 30000 руб. Первому результату благоприятствует 47 случаев, второму результату - два случая и третьему – один случай. Найдем их вероятности:
представляет собой выигрыш и может принимать три значения: 0, 5000 и 30000 руб. Первому результату благоприятствует 47 случаев, второму результату - два случая и третьему – один случай. Найдем их вероятности: 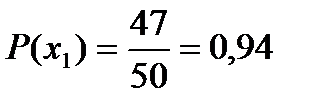 ;
; 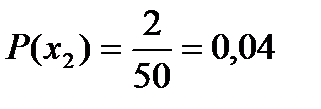 ;
;  .
.
Закон распределения случайной величины имеет вид:
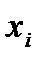
| |||
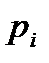
| 0,94 | 0,04 | 0,02 |
В качестве проверки найдем 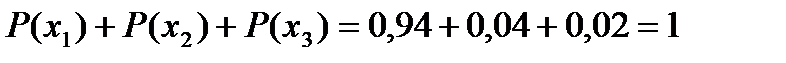 .
.
Дата добавления: 2014-12-05; просмотров: 1195;
