Математическое ожидание дискретной случайной величины
Наиболее исчерпывающей характеристикой случайной величины является ее закон распределения вероятностей. Однако не всегда обязательно знать весь закон распределения. Иногда можно обойтись одним или несколькими числами, отражающими наиболее важные особенности закона распределения, например, числом, имеющим смысл «среднего значения» случайной величины, или же числом, показывающим средний размер отклонения случайной величины от своего среднего значения. Такого рода числа называются числовыми характеристиками случайной величины. Оперируя числовыми характеристиками, можно решать многие задачи, не пользуясь законом распределения.
Одна из самых важных числовых характеристик случайной величины есть математическое ожидание.
Если известна дискретная случайная величина 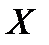 , закон распределения которой имеет вид
, закон распределения которой имеет вид
Значения 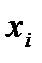
| 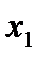
| 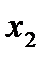
| … | 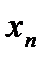
|
Вероятности 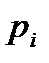
| 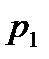
| 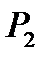
| … | 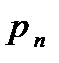
|
то математическим ожиданием (или средним значением) дискретной величины 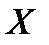 называется число
называется число
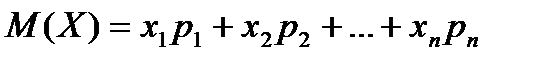 .
.
Таким образом, математическое ожидание дискретной случайной величины 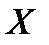 равно сумме произведений возможных значений этой величины на их вероятности.
равно сумме произведений возможных значений этой величины на их вероятности.
Пример 1. Найти математическое ожидание случайной величины 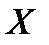 , зная закон ее распределения
, зная закон ее распределения
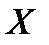
| -1 | ||||
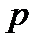
| 0,2 | 0,1 | 0,25 | 0,15 | 0,3 |
Решение.
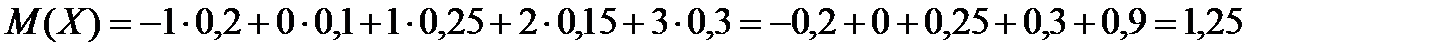 .
.
Свойства математического ожидания.
1. Постоянный множитель можно выносить за знак математического ожидания: 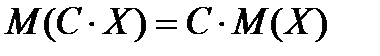
2. Математическое ожидание постоянной величины С равно самой этой величине: 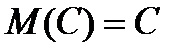
3. Математическое ожидание суммы двух случайных величин равно сумме их математических ожиданий: 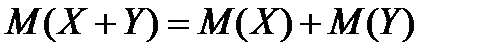 .
.
4. Математическое ожидание произведения независимых случайных величин равно произведению математических ожиданий этих величин: 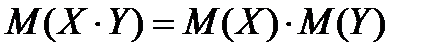 .
.
Дата добавления: 2014-12-05; просмотров: 1614;
