Двумерные случайные величины.
Часто приходится решать задачи, в которых рассматриваются события, описываемые не одной, а несколькими — в частности, двумя случайными величинами. Так если станок-автомат штампует цилиндрические валики, то диаметр валика  и его высота
и его высота  , образуют систему двух случайных величин
, образуют систему двух случайных величин 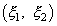
Двумерной случайной величиной называют систему из двух случайных величин 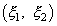 , для которой определена вероятность
, для которой определена вероятность 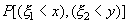 совместного выполнения неравенств
совместного выполнения неравенств 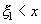 и
и 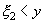 , где x и y - любые действительные числа.
, где x и y - любые действительные числа.
Функция двух переменных
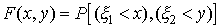
| (34) |
определенная для любых x и y, называется функцией распределения системы двух случайных величин 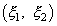
Будем рассматривать  и
и  как декартовы координаты точки на плоскости. Точка
как декартовы координаты точки на плоскости. Точка 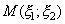 может занимать то или иное положение на плоскости
может занимать то или иное положение на плоскости 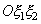 . Тогда функция распределения даст вероятность того, что случайная точка
. Тогда функция распределения даст вероятность того, что случайная точка 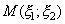 попадает в область
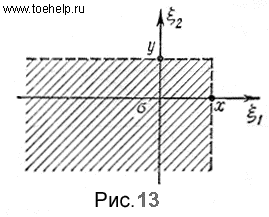
попадает в область 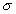 , изображенную на рис. 13.
, изображенную на рис. 13.
Двумерная случайная величина 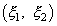 называется дискретной, если
называется дискретной, если  и
и  - дискретные величины.
- дискретные величины.
Пусть возможные значения  и
и  образуют, например, конечные последовательности x1, x2, ..., xn и y1, y2, ..., ys. Возможные значения двумерной случайной величины
образуют, например, конечные последовательности x1, x2, ..., xn и y1, y2, ..., ys. Возможные значения двумерной случайной величины 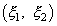 имеют вид (xi, yj), где i=1, 2, ..., n; j=1, 2, ..., s. Обозначим через pij вероятность того, что
имеют вид (xi, yj), где i=1, 2, ..., n; j=1, 2, ..., s. Обозначим через pij вероятность того, что 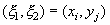
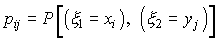
Функция распределения F(х, у) имеет вид
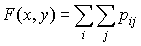
где двойная сумма распространена на те i и j, для которых xi<x и yj<y.
Двумерную случайную величину 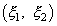 так же, как и одномерную, можно задавать таблицей. Первая строка таблицы содержит возможные значения случайной величины
так же, как и одномерную, можно задавать таблицей. Первая строка таблицы содержит возможные значения случайной величины  , а первый столбец — возможные значения
, а первый столбец — возможные значения  . В остальных клетках таблицы указаны соответствующие вероятности, причем их сумма всегда равна единице. В качестве примера рассмотрим двумерную случайную величину, заданную следующей таблицей:
. В остальных клетках таблицы указаны соответствующие вероятности, причем их сумма всегда равна единице. В качестве примера рассмотрим двумерную случайную величину, заданную следующей таблицей:
 \ \ 
| -1 | 0 | 1 |
| 0,1 | p11=0,05 | p12=0,20 | p13=0,30 |
| 0,2 | p21=0,10 | p22=0,20 | p23=0,15 |
Сумма всех вероятностей
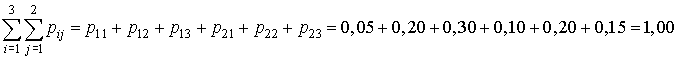
Две дискретные случайные величины  и
и  называются независимыми, если для всех пар i, j выполняется соотношение
называются независимыми, если для всех пар i, j выполняется соотношение
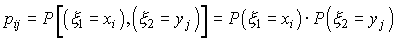
Пример 1. Две игральные кости бросают по одному разу. Обозначим через  число очков, выпавшее на первой кости, а через
число очков, выпавшее на первой кости, а через  — на второй; тогда
— на второй; тогда 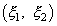 — Двумерная дискретная величина. Покажем, что величины
— Двумерная дискретная величина. Покажем, что величины  и
и  независимы. (Решение)
независимы. (Решение)
Двумерная величина 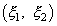 называется непрерывной, если существует такая непрерывная неотрицательная функция
называется непрерывной, если существует такая непрерывная неотрицательная функция 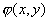 , двух переменных, что вероятность того, что точка
, двух переменных, что вероятность того, что точка 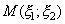 содержится в некоторой области
содержится в некоторой области 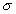 плоскости
плоскости 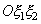 , равна двойному интегралу от функции
, равна двойному интегралу от функции 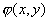 по области
по области 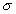 :
:
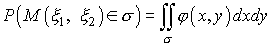
| (35) |
Функция 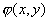 называется плотностью распределения вероятностей системы двух величин
называется плотностью распределения вероятностей системы двух величин  и
и  . Отсюда, в частности, следует, что если область
. Отсюда, в частности, следует, что если область 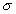 имеет вид, изображенный на рис. 13, то функцию распределения системы случайных величин можно записать следующим образом:
имеет вид, изображенный на рис. 13, то функцию распределения системы случайных величин можно записать следующим образом:
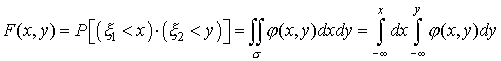
| (36) |
Непрерывные случайные величины  и
и  называются независимыми, если
называются независимыми, если  , где
, где 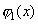 и
и 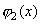 - соответственно плотности распределения вероятностей случайных величин
- соответственно плотности распределения вероятностей случайных величин  и
и  . В этом случае
. В этом случае
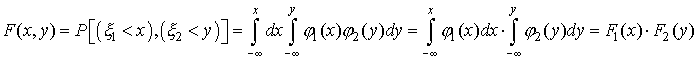
где F1(x) и F2(y) — соответственно функции распределения величин  и
и  [см. формулу (22)].
[см. формулу (22)].
Зная функцию распределения F(х,у) двумерной случайной величины 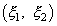 , легко найти как функцию распределения, так и плотность распределения каждой из случайных величин
, легко найти как функцию распределения, так и плотность распределения каждой из случайных величин  и
и  , в отдельности.
, в отдельности.
Действительно, пусть F1(x) - функция распределения случайной величины  . Тогда
. Тогда 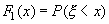 . Так как в этом случае
. Так как в этом случае  может принимать любое значение, то ясно, что
может принимать любое значение, то ясно, что
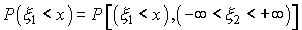
Следовательно, по формуле (36) имеем
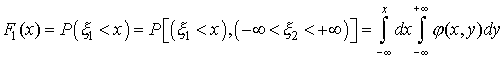
Дифференцируя последнее равенство по x, согласно правилу дифференцирования интеграла по переменной верхней границе получим
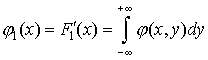
| (37) |
Аналогичным образом получаем
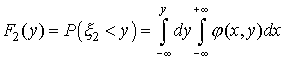
и, следовательно,
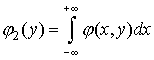
| (38) |
Таким образом, чтобы получить плотность распределения одной из составляющих двумерной случайной величины, надо проинтегрировать в границах от 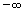 до
до 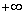 плотность распределения системы
плотность распределения системы 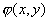 по переменной, соответствующей другой случайной величине.
по переменной, соответствующей другой случайной величине.
Пример 2. Двумерная случайная величина 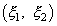 имеет плотность распределения
имеет плотность распределения
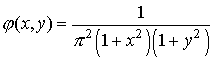
Найти:
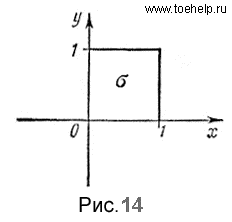
1) вероятность р попадания случайной точки 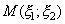 в квадрат изображенный на рис. 14;
в квадрат изображенный на рис. 14;
2) функцию распределения F(х,у);
3) плотности распределения каждой величины  и
и  в отдельности. (Решение)
в отдельности. (Решение)
По определению двумерная случайная величина 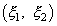 распределена нормально, если плотность распределения системы величин
распределена нормально, если плотность распределения системы величин  и
и  имеет вид
имеет вид

где 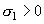 ,
, 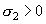 , а R - некоторая постоянная (см. § 9, п. 2). Можно показать [используя формулы (37) и (38)], что каждая из величин
, а R - некоторая постоянная (см. § 9, п. 2). Можно показать [используя формулы (37) и (38)], что каждая из величин  и
и  распределена нормально:
распределена нормально:
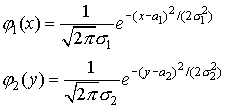
На доказательстве этого факта мы не будем останавливаться. В частности, если  и
и  независимы, то
независимы, то 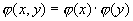 . Отсюда следует, что R=0, и, cледовательно,
. Отсюда следует, что R=0, и, cледовательно,
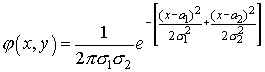
Нетрудно убедиться в том, что справедливо и обратное утверждение: если R=0, то  и
и  — независимые случайные величины.
— независимые случайные величины.
Дата добавления: 2014-11-29; просмотров: 1323;
