Бозе-эйнштейна распределение
В статистической механике статистика Бо́зе — Эйнште́йна определяет распределение тождественных частиц с нулевым или целочисленным спином (таковыми являются, например, фотоны и атомы гелия-4) по энергетическим уровням в состояниитермодинамического равновесия. Предложена в 1924 году Шатьендранатом Бозе для описания фотонов. В 1924—1925 годах Альберт Эйнштейн обобщил её на системы атомов с целым спином.
В классической физике распределение частиц по энергиям описывается хорошо известными из курса молекулярной физики распределением Максвелла
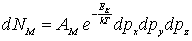
| (6.31a) |
и распределением Больцмана
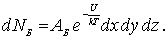
| (6.31b) |
Здесь 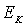 и
и 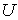 - соответственно кинетическая и потенциальная энергии частицы,
- соответственно кинетическая и потенциальная энергии частицы, 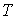 - температура,
- температура, 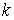 - постоянная Больцмана,
- постоянная Больцмана, 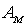 и
и 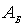 - нормировочные константы.
- нормировочные константы.
Напомним, что при выводе статистических распределений отыскивается наиболее вероятное распределение частиц, т.е. распределение, которое может быть реализовано наибольшим числом способов. Согласно основному постулату статистической физики именно это распределение является равновесным. Будем считать, что частицы не взаимодействуют друг с другом ( модель идеального газа), а также полагать, что все распределения, которые приводят к одной и той же суммарной энергии частиц, реализуются с одинаковой вероятностью.
При выводе распределений в классической физике считается, что одинаковые частицы принципиально различимы. Это, в частности, приводит к тому, что распределение, в котором одна из двух одинаковых частиц - частица 1 - находится в состоянии 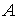 , а другая - частица 2 - в состоянии
, а другая - частица 2 - в состоянии 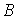 , и распределение, в котором частица 1 находится в состоянии
, и распределение, в котором частица 1 находится в состоянии 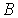 , а частица 2 - в состоянии
, а частица 2 - в состоянии 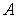 , являются двумя разными распределениями. В квантовой механике в силу тождественности одинаковых частиц эти два распределения следует считать одним распределением. Кроме того, из-за различия в свойствах ферми- и бозе-частиц, статистические распределения для этих частиц должны существенно различаться друг от друга.
, являются двумя разными распределениями. В квантовой механике в силу тождественности одинаковых частиц эти два распределения следует считать одним распределением. Кроме того, из-за различия в свойствах ферми- и бозе-частиц, статистические распределения для этих частиц должны существенно различаться друг от друга.
Проиллюстрируем различие в распределении классических и квантовых частиц (фермионов и бозонов) на следующем примере. Пусть нам нужно распределить две частицы по трем состояниям (ячейкам). Классические частицы, в силу их различимости, будем отмечать номерами 1 и 2 . Квантовые частицы одного сорта принципиально неразличимы, будем изображать их черными кружочками. При этом ферми-частицы, в соответствие с запретом Паули, могут находиться в каждой ячейке только поодиночке, что же касается бозе-частиц, то никаких ограничений на распределение их по ячейкам не накладывается. Результаты распределения приведены на рисунке 6.1а.
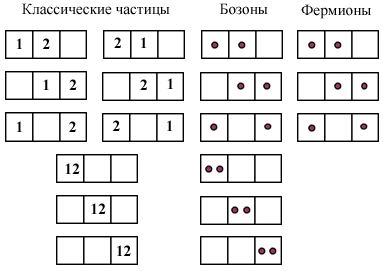
|
| Рис. 6.1a. |
Для классических частиц число возможных распределений (микросостояний) равно девяти, а вероятность каждого из них - 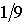 . Для бозе-частиц получается шесть распределений, соответственно вероятность каждого из них равна
. Для бозе-частиц получается шесть распределений, соответственно вероятность каждого из них равна 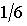 . Для ферми-частиц реализуются только три распределения с вероятностью выпадения каждого из них, равной
. Для ферми-частиц реализуются только три распределения с вероятностью выпадения каждого из них, равной 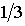 .
.
Вывод распределения Бозе-Эйнштейна. Приступим теперь к выводу закона распределения бозе-частиц по энергиям. Предварительно решим следующую вспомогательную задачу. Пусть имеется длинный пенал, который может быть разделен на 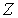 ячеек с помощью
ячеек с помощью 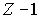 перегородки (рис.6.2 ) . Найдем число способов, с помощью которых
перегородки (рис.6.2 ) . Найдем число способов, с помощью которых 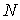 неразличимых
неразличимых
частиц могут быть распределены по ячейкам этого пенала. Поскольку мы имеем дело с бозе-частицами, то будем считать, что в каждой ячейке может находиться произвольное число частиц.

|
| Рис. 6.2. |
Таким образом, наша система состоит из 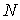 частиц и
частиц и 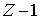 перегородки, т.е. из
перегородки, т.е. из 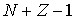 элементов. Рассмотрим все возможные перестановки элементов этой системы. Следует отметить, что речь идет не только о перестановке частиц с частицами, но и перегородок с перегородками, что меняет нумерацию ячеек и, вообще говоря, число частиц в них . Кроме того, могут переставляться перегородки вместе с частицами, что приводит к изменению нумерации ячеек. Общее число таких перестановок, согласно комбинаторике, равно
элементов. Рассмотрим все возможные перестановки элементов этой системы. Следует отметить, что речь идет не только о перестановке частиц с частицами, но и перегородок с перегородками, что меняет нумерацию ячеек и, вообще говоря, число частиц в них . Кроме того, могут переставляться перегородки вместе с частицами, что приводит к изменению нумерации ячеек. Общее число таких перестановок, согласно комбинаторике, равно 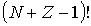 . Однако не все они приводят к новым распределениям. Так, перестановки частиц из-за их неразличимости ничего не меняют. Число таких перестановок равно
. Однако не все они приводят к новым распределениям. Так, перестановки частиц из-за их неразличимости ничего не меняют. Число таких перестановок равно 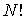 . Перестановки только перегородок тоже не приводят к новым распределениям, их число равно
. Перестановки только перегородок тоже не приводят к новым распределениям, их число равно 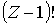 . Таким образом, число способов
. Таким образом, число способов 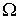 , с помощью которых
, с помощью которых 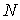 тождественных частиц могут быть распределены по
тождественных частиц могут быть распределены по 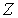 ячейкам, равно
ячейкам, равно
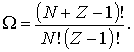
| (6.32) |
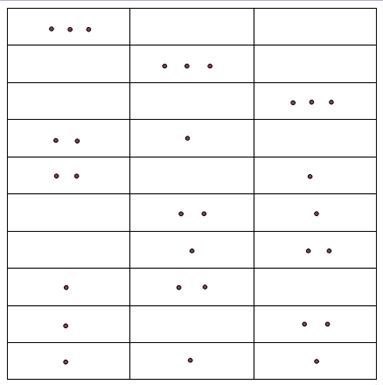
Проиллюстрируем полученный результат на следующем примере. Рассмотрим возможные распределения трех частиц по трем ячейкам. (рис.6.3 ). Всего таких распределений 10 . Точно такой же результат дает
|
| Рис. 6.3. |
выражение (6.32) при 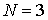 и
и 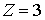
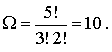
Поскольку считалось, что в ячейке может находится любое число частиц, то выражение (6.32) определяет число способов, с помощью которых 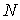 бозонов могут быть распределены по
бозонов могут быть распределены по 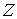 состояниям. Каждый способ размещения частиц представляет собой определенное микросостояние системы. Следовательно,
состояниям. Каждый способ размещения частиц представляет собой определенное микросостояние системы. Следовательно, 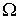 определяет число микросостояний, с помощью которых реализуется конкретное макросостояние системы. Таким образом,
определяет число микросостояний, с помощью которых реализуется конкретное макросостояние системы. Таким образом, 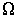 есть термодинамическая вероятность или статистический весмакросостояния системы.
есть термодинамическая вероятность или статистический весмакросостояния системы.
Рассмотрим шестимерное фазовое пространство с координатами 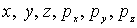 . В этом пространстве уравнение
. В этом пространстве уравнение
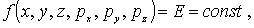
где 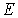 - энергия частицы, определяет изоэнергетическую поверхность, т.е. поверхность, все точки которой отвечают одному и тому же значению энергии частицы.
- энергия частицы, определяет изоэнергетическую поверхность, т.е. поверхность, все точки которой отвечают одному и тому же значению энергии частицы.
Разобьем с помощью изоэнергетических поверхностей фазовое пространство на тонкие энергетические слои. Пусть 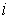 - ый слой ограничен поверхностями
- ый слой ограничен поверхностями
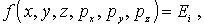
и
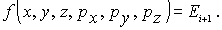
Будем считать слой тонким, если 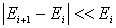 . В этом случае энергию всех частиц, попадающий в
. В этом случае энергию всех частиц, попадающий в 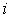 - ый слой, можно считать одинаковой и равной
- ый слой, можно считать одинаковой и равной 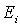 .
.
Пусть объем 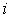 - го слоя равен
- го слоя равен 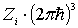 . С учетом (6.26) это означает, что число квантовых состояний (ячеек) для этого слоя равно
. С учетом (6.26) это означает, что число квантовых состояний (ячеек) для этого слоя равно 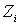 . Число частиц в пределах
. Число частиц в пределах 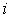 - го слоя будем считать равным
- го слоя будем считать равным 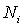 . Тогда, согласно (6.32) , статистический вес подсистемы, содержащей
. Тогда, согласно (6.32) , статистический вес подсистемы, содержащей 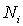 частиц, равен
частиц, равен
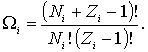
Статистический вес всей системы равен произведению статистических весов отдельных ее подсистем
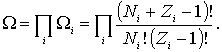
| (6.33) |
Как уже отмечалось, нас интересует распределение, которое может быть реализовано наибольшим числом способов, т.е. распределение, для которого статистический вес 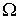 максимален. Таким образом, нужно найти максимум выражения (6.33) . При этом следует иметь в виду, что полное число частиц системы
максимален. Таким образом, нужно найти максимум выражения (6.33) . При этом следует иметь в виду, что полное число частиц системы
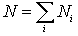

и полная энергия системы
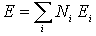
должны оставаться постоянными.
Исследование на экстремум выражения (6.33) представляет собой достаточно сложную задачу, поэтому вместо максимума статистического веса 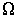 будем искать максимум энтропии
будем искать максимум энтропии 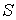 , которая связана со статистическим весом соотношением
, которая связана со статистическим весом соотношением
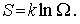
| (6.34) |
Подставляя (6.32) в (6.34) , получаем
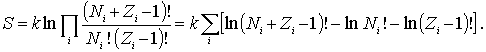
Для дальнейших преобразований воспользуемся формулой Стирлинга, согласно которой при 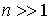
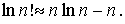
Считая, что 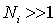 и
и 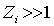 , получаем
, получаем
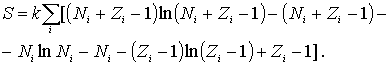
Перепишем это выражение в виде
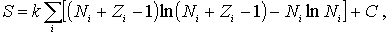
| (6.35) |
где 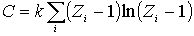 . Слагаемое
. Слагаемое 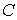 в (6.35) не зависит от числа частиц
в (6.35) не зависит от числа частиц 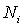 , поэтому при отыскании максимума функции
, поэтому при отыскании максимума функции 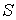 его можно не учитывать, т.к. в задаче на экстремум будет варьироваться только число частиц в слое
его можно не учитывать, т.к. в задаче на экстремум будет варьироваться только число частиц в слое 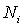 .
.
Для отыскания максимума энтропии (6.35) при условии постоянства числа частиц системы 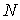 и энергии
и энергии 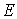 воспользуемся методом множителей Лагранжа. Этот метод заключается в следующем. Пусть нам нужно найти экстремум функции
воспользуемся методом множителей Лагранжа. Этот метод заключается в следующем. Пусть нам нужно найти экстремум функции
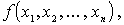
аргументы которой удовлетворяют условиям
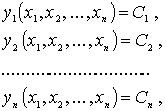

где 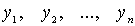 - некоторые известные функции, а
- некоторые известные функции, а 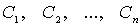 - константы. Для этого, согласно методу Лагранжа, нужно построить функцию
- константы. Для этого, согласно методу Лагранжа, нужно построить функцию
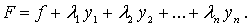
Здесь 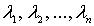 - постоянные коэффициенты, называемые множителями Лагранжа. Затем следует взять частные производные функции
- постоянные коэффициенты, называемые множителями Лагранжа. Затем следует взять частные производные функции 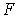 по всем переменным
по всем переменным 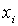 и приравнять их нулю. В итоге получаем систему
и приравнять их нулю. В итоге получаем систему 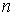 уравнений, решение которой дает нам значения переменных
уравнений, решение которой дает нам значения переменных 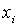 , при которых достигается условный экстремум.
, при которых достигается условный экстремум.
Напомним, что в нашей задаче переменной величиной является число частиц 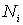 , а дополнительно накладываемые условия сводятся к требованию постоянства числа частиц системы
, а дополнительно накладываемые условия сводятся к требованию постоянства числа частиц системы 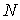 и энергии
и энергии 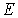 . Поэтому функция
. Поэтому функция 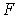 в данном случае имеет вид
в данном случае имеет вид
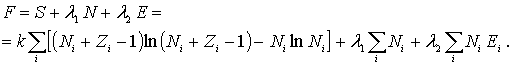

Приравнивая производную 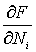 нулю, получаем
нулю, получаем
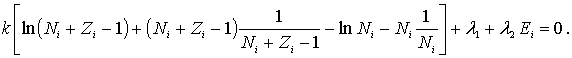
Преобразуем это выражение к виду
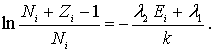

Отсюда следует, что
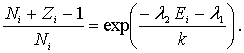

Разделим числитель и знаменатель левой части полученного равенства на 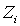
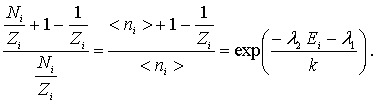
Отношение 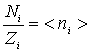 представляет собой среднее число частиц, приходящихся на одну ячейку фазового пространства, т.е. на одно состояние в
представляет собой среднее число частиц, приходящихся на одну ячейку фазового пространства, т.е. на одно состояние в 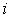 - ом энергетическом слое.
- ом энергетическом слое.
Поскольку 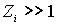 , то слагаемым
, то слагаемым 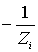 в числителе можно пренебречь. Таким образом для
в числителе можно пренебречь. Таким образом для 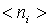 получаем
получаем
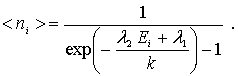
Найдем теперь выражения для множителей Лагранжа 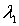 и
и 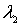 . Множитель
. Множитель 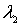 можно отыскать следующим образом. Поскольку все частные производные функции
можно отыскать следующим образом. Поскольку все частные производные функции 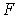 по
по 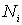 равны нулю, то это означает, что равен нулю дифференциал этой функции
равны нулю, то это означает, что равен нулю дифференциал этой функции 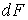 , т.е.
, т.е.
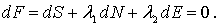
Но так как число частиц системы 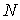 постоянно, то
постоянно, то 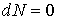 и, следовательно,
и, следовательно,
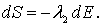
| (6.36) |
Предположим теперь, что рассматриваемая система получает в обратимом процессе некоторое количество теплоты 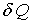 при неизменном объеме
при неизменном объеме 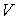 . В результате этого энтропия системы получает приращение
. В результате этого энтропия системы получает приращение
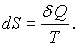
Поскольку 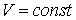 , то работа при получении теплоты не совершается и
, то работа при получении теплоты не совершается и
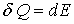 , следовательно,
, следовательно,
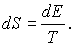
| (6.37) |
Сравнивая (6.36) и (6.37) , находим, что 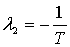 .
.
Множитель 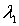 представим в виде
представим в виде
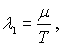
| (6.38) |
где 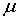 - некоторая функция параметров состояния системы, в частности, температуры. Эту функцию называют химическим потенциалом. Понятие химического потенциала оказывается очень важным для анализа термодинамического равновесия систем: одним из условий равновесия является равенство химического потенциала для всех частей системы.
- некоторая функция параметров состояния системы, в частности, температуры. Эту функцию называют химическим потенциалом. Понятие химического потенциала оказывается очень важным для анализа термодинамического равновесия систем: одним из условий равновесия является равенство химического потенциала для всех частей системы.
С учетом выражений для 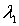 и
и 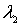
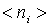 принимает вид
принимает вид
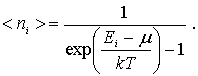
Освобождаясь от индекса 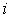 , окончательно получаем
, окончательно получаем
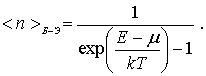
| (6.39) |
Выражение (6.39) называется распределением Бозе-Эйнштейна. Оно описывает распределение бозе-частиц по энергиям и определяет среднее число бозе-частиц 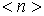 , находящихся в квантовом состоянии с энергией
, находящихся в квантовом состоянии с энергией 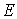 . Величину называют также числом заполнения энергетического уровня с энергией
. Величину называют также числом заполнения энергетического уровня с энергией 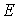
Дата добавления: 2014-12-06; просмотров: 2134;
