Спин электрона, нейтрино и других элементарных частиц.

Спин (англ. spin, букв.-вращение), собственный момент количества движения элементарной частицы (электрона,протона и т. п.). Имеет квантовую природу и не связан с какими-либо перемещениями частицы, в том числе не зависит от наличия или отсутствия у нее орбитального (углового) момента количества движения. Пространственное квантование спина определяет квантовое число s: проекция спина S частицы на выбранное направление S_z может принимать значения, измеряемые в единицах постоянной Планка ђ и равные — sђ, —sђ + ђ, ..., sђ. Квантовое число sназывают спиновым квантовым числом или просто спин; оно равно для электрона, протона, нейтрона. нейтрино 1/2, для фотона 1, для p- и К-мезонов 0.

Спином называют также собственный момент количества движения атомного ядра. атома, молекулярной системы; в этом случае спин системы определяется как векторная сумма спинов отдельных частиц: Ss = S. Так, спин ядра равен целому или полуцелому числу (обозначается обычно I) в зависимости от того, включает ли ядро четное или нечетное число протонов и нейтронов. Например, для ¹Н I = 1/2, для ¹⁰В I = 3, для ¹¹В I = 3/2, для ¹⁷О I = 5/2, для ¹⁶О I = 0. Для атома Не в основном состоянии полный электронный спин S = 0, в первом возбужденном состоянии S = 1. В современной теоретической физике, главным образом в теории элементарных частиц, спин-часто называют полный момент количества движения частицы, равный сумме орбитального и собств. моментов.

Концепция спина введена в 1925 Дж. Уленбеком и С. Гаудсмитом, которые для интерпретации экспериментальных данных о расщеплении пучка атомов серебра в магнитном поле предположили, что электрон можно рассматривать как вращающийся вокруг своей оси волчок с проекцией на направление поля, равной 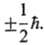В том же году В. Паули ввел понятие спин в математический аппарат нерелятивистской квантовой механики и сформулировал принцип запрета, утверждающий, что две тождественные частицы с полуцелым спином не могут одновременно находиться в системе в одном и том же квантовом состоянии). Согласно подходу В. Паули, существуют операторы s² и s_z, которые обладают собственными значениями ђ²s(s + 1) и ђs_z соответственно и действуют так называемые спиновые части волновой функции a и b (спин-функции) так же, как операторы орбитального момента количества движения I² и I_z действуют на пространств. часть волновой функции Y(r), где r-радиус-вектор частицы. Операторы s² и s_z подчиняются тем же правилам коммутации, что и операторы I² и I_z.

Уравнение Дирака. В 1928 П. Дираком было показано, что существование спина следует из релятивистского (с учетом конечности скорости света) решения задачи о движении электрона в электромагнитном поле. Уравнение Дирака имеет формально такой же вид, что и уравнение Шрёдингера:

iђdY_D/dt = H_DY_D

(t-время). Оператор H_D, однако, линеен по компонентам импульса электрона р, и если напряженность поля характеризуется векторным потенциалом А с компонентами А_х, А_у, А_z и скалярным потенциалом V, то

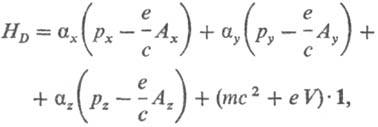
где е и m-заряд и масса покоя электрона, с-скорость света. Операторы р_х, р_у, р_z имеют обычный вид:

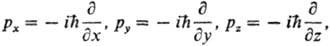
коэффициенты a_x, a_у, a_z-матрицы размера 4 x 4 (матрицы Дирака), 1-единичная матрица. Релятивистская волновая функция Y_D для электрона, как и для любой другой частицы с спин 1/2, должна быть 4-компонентной; обычно это выражают следующей записью:

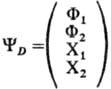
Уравнение Дирака фактически является системой 4 уравнений для 4 функций F_i и X_i, зависящих от координат х, у и z и времени t.

Существование спина как собственного момента количества движения электрона следует из того, что в отсутствие момента внеш. сил оператор H_D коммутирует не с оператором орбитального момента L, как оператор H в уравнении Шрёдингера, а с оператором J = L + S. Это значит, что не сохраняется орбитальный момент количества движения свободного электрона, а сохраняется лишь сумма орбитального и некоторого дополнительного момента-спина.

Уравнение Дирака существенно упрощается при малых (относительно скорости света) скоростях u классического движения электрона, когда 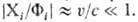В нерелятивистском пределе, когда масса электрона становится равной массе покоя, X₁ и Х₂ устремляются к нулю, а оператор H_D переходит в так называемый оператор Брейта-Паули:

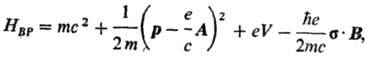
где s • В = s_xВ_х + s_gВ_у + s_zВ_z; В_х, В_у, В_z - компоненты вектора магнитной индукции В = rot А, совпадающие в вакууме с компонентами напряженности магнитного поля Н, а s_x, s_y, s_z-матрицы размера 2x2 (матрицы Паули):

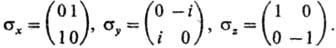
Волновая функция Y_ВP, являющаяся решением уравнения Брейта-Паули, имеет два компонента, в отличие от 4-компонентной Y_D:

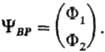
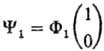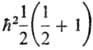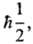Для электрона в однородном магнитном поле Y_ВP всегда может быть представлена как собственная функция операторов s² и s_z с собственными значениями ђ²s(s + 1) и bђs, где s = 1/2. Таких собственных функций две: одна с собственными значениями и другая 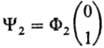с собств. значениям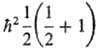и и — 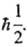Эти функции обычно записывают в виде:

Y₁=F₁(r,t)a и Y₂ = F₂(r,t)b,

где под символаaми a и b имеют в виду векторы 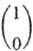и 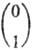, которые и называют спин-функциями. Говорить об их функциональной зависимости можно лишь условно, и часто встречающаяся запись вида a(1) b(2) означает только то, что символ a представляет собой вектор для одного электрона, а символ b-соответствующий вектор для второго электрона.

Спиновый магнитный момент. В оператор Брейта-Паули Н_ВР входят два члена, линейно зависящие от компонент векторного потенциала А, определяющего внешнее магнитное поле:

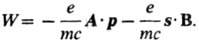
Для однородного поля А = 1/2 В x r, знак x означает векторное произведение, и

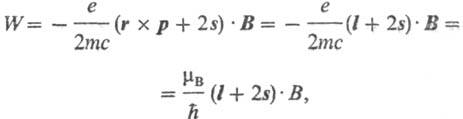
где 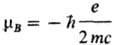-магнетон Бора. Векторная величина 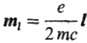называют магнитным моментом частицы с зарядом е и массой т (в данном случае-электрона), векторная же величина 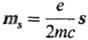получила название спинового магнитного момента. Отношение коэффициентов перед s и l наз. g-фактором частицы. Для протона ¹Н (спинI = 1/2) g-фактор равен 5,5854, для ядра ¹³С с тем же спин I = 1/2 g-фактор равен 1,4042; возможны и отрицательныйg-факторы, например: для ядра ²⁹Si g-фактор равен — 1,1094 (спин равен 1/2). Экспериментально определяемая величина g-фактора электрона составляет 2,002319.

Как для одного электрона, так и для системы электронов или других частиц спин 5 ориентируется относительно направления однородного поля. Проекция спин S_z на направление поля принимает 2S + 1 значение: — S, — S + 1, ... ,S. Число различных проекций спин называют мультиплетностью квантового состояния системы со спином S.

Магнитное поле, действующее на электрон или ядро в молекуле, может быть не только внешним, оно может создаваться и другими электронами либо возникать при вращении системы заряженных частиц как целого. Так, взаимодействие магнитного поля, создаваемого электроном i, с ядром v приводит к появлению в гамильтониане члена вида:

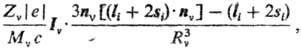
где n_v- единичный вектор в направлении радиуса-вектора ядра R_v, Z_v и М_v-заряд и масса ядра. Члены вида I_v•I_iотвечают спин-орбитальному взаимодействию, члены вида I_v•s_i- спин-спиновому взаимодействию. Для атомных и мол. систем наряду с указанными возникают и члены, пропорциональные (s_i•s_j), (I_v•I_m) и т.п. Эти члены обусловливают расщепление вырожденных энергетических уровней, а также приводят к различным сдвигам уровней, что определяет тонкую структуру и сверхтонкую структуру.

Экспериментальные проявления спин Наличие отличного от нуля спин электронной подсистемы приводит к тому, что у молекулы в однородном магнитном поле наблюдается расщепление уровней энергии, причем на величину этого расщепления влияет хим. строение молекулы. Наличие ненулевых спинов атомных ядер также приводит к расщеплению уровней, причем это расщепление зависит от экранирования внеш. поля ближайшим к данному ядру окружением. Спин-орбитальное взаимодействие приводит к сильным расщеплениям уровней электронных состояний, достигающим величин порядка нескольких десятых эВ и даже нескольких единиц эВ. Особенно сильно оно проявляется у атомов тяжелых элементов, когда становится невозможным говорить о том или ином спин атома или молекулы, а можно говорить лишь о полном моменте импульса системы. Более слабыми, но, тем не менее, отчетливо устанавливаемыми при исследовании спектров являются спин-вращательные и спин-спиновые взаимодействия. Для конденсированных сред наличие спин частиц проявляется в магнитных свойствах этих сред. При определенной температуре возможно возникновение упорядоченного состояния спин частиц (атомов, молекул, ионов), находящихся, например, в узлах кристаллической решетки, а следовательно, и связанных с спином магнитных моментов, что ведет к появлению у системы сильного парамагнетизма (ферромагнетизма, антиферромагнетизма). Нарушение упорядоченности спин частиц проявляется в виде спиновых волн. Взаимодействие собственных магнитных моментов с упругими колебаниями среды называют спин-фононным взаимодействием, оно определяет спин-решеточную релаксацию и спин-фононное поглощение звука.

Важное проявление спин-связанные с ним правила отбора и правила запрета. При слабом спин-орбитальном либо спин-спиновом взаимодействии у системы сохраняются по отдельности орбитальный момент и спин либо спины тех или иных подсистем. Так, можно говорить об определенном спин подсистемы ядер и подсистемы электронов молекулы. Слабое спин-спиновое взаимодействие электронов и излучаемого (или поглощаемого) молекулой фотона приводит к тому, что спин электронной подсистемы с большой вероятностью не меняется при излучении (поглощении) света, что приводит к правилу отбора при квантовых переходах: излучение или поглощение света происходит так, что спин молекулы сохраняется, т. е. DS = 0. Сохранение спин приводит и к тому, что излучательное время жизни атомов и молекул, находящихся, например, в низшем возбужденном триплетном состоянии, оказывается очень большим из-за запрета по спину излучательного перехода в основное синглетное состояние. В газофазных химических реакциях часто выполняется аналогичное правило: в ходе элементарного акта взаимодействия частиц суммарный спин системы не меняется. Изучение правил запрета по спину и выяснение причин, вызывающих их нарушения, позволяет получать важную информацию о механизмах реакций и роли спиновых эффектов в реакциях.

Спин и химическая связь. На начальном этапе развития квантовой химии В. Гайтлером и Ф. Лондоном при рас-смотрении молекулы Н₂ образование хим. связи было соотнесено со способностью электрона одного атомаобразовывать пару с противоположным по спин электроном др. атома. Таким образом возникла теория двухэлектронных связей, послужившая основой квантовохимического расчетного метода локализованных электронных пар. Аналогичный вывод о том, что образование хим. связи обусловлено тенденцией к спариванию спин электронов, впоследствии был сформулирован в молекулярных орбиталей методах. Это утверждение является весьма приближенным. Его качественная справедливость может быть обоснована лишь в тех случаях, когда для описания электронного состояния системы можно с хорошей точностью использовать пробную волновую функцию, отвечающую всего лишь одной валентной схеме, либо функцию ограниченного метода Хартри-Фока. В целом влияние спина на образование химической связи оказывается лишь косвенным: требование антисимметричности электронной волновой функции приводит при заданном спин молекулы к определенным ограничениям на пространственное распределение электронов, что влечет за собой и различие в энергиях состояний с разной мультиплетностью.