Знакопеременные и знакочередующиеся ряды
Ряды, содержащие как положительные, так и отрицательные члены, называются знакопеременными.
Пусть дан знакопеременный ряд
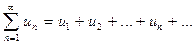 . (4)
. (4)
Рассмотрим знакоположительный ряд, состоящий из модулей членов ряда (4):
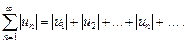 (5)
(5)
Ряд (4) сходится, если сходится ряд (5). В этом случае ряд (4) называется абсолютно сходящимся. Если же ряд (4) сходится, а ряд (5) расходится, то ряд (4) называется условно сходящимся.
Частным случаем знакопеременного ряда является знакочередующийся ряд
u1 – u2 + …+ (–1)n+1 un + … = 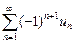 (6)
(6)
(un > 0, n = 1, 2, …),
в котором положительные и отрицательные члены следуют друг за другом поочередно.
Для знакочередующихся рядов имеет место достаточный признак сходимости.
Теорема (признак Лейбница)
Знакочередующийся ряд (6) сходится, если:
1. Последовательность абсолютных величин членов ряда монотонно убывает, т. е. 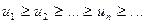 .
.
2. Общий член ряда стремится к нулю, т. е. 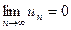 .
.
При этом остаток Rn = S – Sn не превосходит по модулю первого отбрасываемого члена 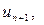 т. е.
т. е. 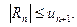
Дата добавления: 2014-12-02; просмотров: 1314;
