Типовая задача 4
Написать степенной ряд по заданному общему члену

Найти область сходимости этого ряда.
Решение. При n = 0 получаем свободный член a0 = 1 данного ряда, при n = 1 — член 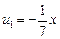 , при n = 2 — член
, при n = 2 — член 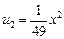 и т. д.
и т. д.
Получаем следующий ряд:
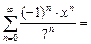

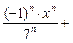 … .
… .
Находим радиус сходимости данного ряда. Имеем:
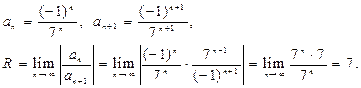
Следовательно, (–7; 7) — интервал сходимости ряда. Исследуем поведение ряда на концах интервала сходимости, т. е. при x = –7,
x = 7.
Пусть x = –7. Тогда степенной ряд принимает вид
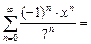
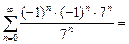
 1 + 1 + …+ 1 + … .
1 + 1 + …+ 1 + … .
Так как 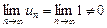 , то ряд расходится (достаточное условие расходимости числового ряда).
, то ряд расходится (достаточное условие расходимости числового ряда).
Пусть x = 7. Получаем следующий знакочередующийся ряд:
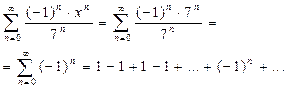
Этот ряд расходится, так как не существует предела последовательности 1,0,1,0… частичных сумм этого ряда.
Таким образом, (–7; 7) — область сходимости данного степенного ряда.
Ответ: (–7; 7).
Типовая задача 5
Вычислить определенный интеграл 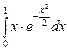 с точностью до 0,001, используя разложение подынтегральной функции в ряд Маклорена.
с точностью до 0,001, используя разложение подынтегральной функции в ряд Маклорена.
Решение. Воспользуемся разложением функции ex:
ex = 1 + x + 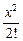 + … +
+ … + 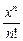 + … .
+ … .
Заменив x на 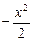 , получим:
, получим:
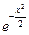 = 1 –
= 1 – 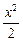 +
+ 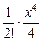 – … +
– … + 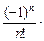
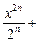 … .
… .
Умножая обе части последнего равенства на x, будем иметь:
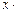
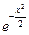 = x –
= x – 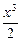 +
+  …+
…+ 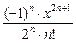 +… .
+… .
Итак, 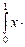
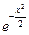 dx =
dx = 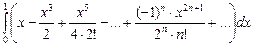 =
=
=  =
=  –
– 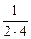 +
+ 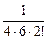 –
–
– … + 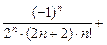 … =
… =  –
– 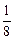 +
+ 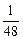 – … +
– … + 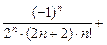 … .
… .
Получаем знакочередующийся ряд. По признаку Лейбница имеем:
1.  .
.
2. 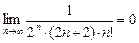 .
.
Значит, ряд сходится. По этому признаку первый отбрасываемый член по модулю меньше un+1. Если un+1 взять по модулю меньшим, чем 0,001, то из 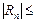 un+1 < 0,001 следует, что остаток Rn меньше 0,001. Имеем:
un+1 < 0,001 следует, что остаток Rn меньше 0,001. Имеем:
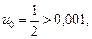
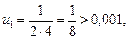
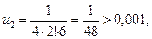
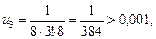
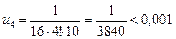 .
.
Значит, 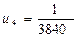 — первый отбрасываемый член.
— первый отбрасываемый член.
Таким образом, с точностью до 0,001

Ответ: 0,393.
4. Задания 6 и 7
по теме «Обыкновенные дифференциальные уравнения»
Дата добавления: 2014-12-02; просмотров: 1111;
