Задача Коши и ее решение

Пусть дано дифференциальное уравнение

. (2)

Задача Коши для данного дифференциального уравнения состоит в следующем: среди всего множества частных решений, которые получаются из общего решения y = 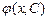при конкретных значениях произвольной постоянной C, следует найти такое частное решение
y = , которое удовлетворяет начальному условию y(x₀) = y₀.

Геометрически задача Коши состоит в выборе среди всего множества интегральных кривых такой кривой, которая проходит через точку M₀(x₀, y₀) (рис. 20).

Рис. 20

Теорема (существования и единственности решения задачи Коши). Если в дифференциальном уравнении (2) функция f(x,y) и
ее частная производная непрерывны в некоторой области,
содержащей точку (x₀,y₀), то решение дифференциального уравне-
ния (2) при начальном условии y(x₀) = y₀ существует и оно единственно.