Линейное однородное дифференциальное уравнение второго порядка

Так называется уравнение вида

(4)

Функции y₁(x), y₂(x) называются линейно независимыми, если равенство

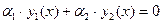(5)

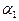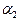( , — постоянные) возможно лишь в случае .

Если хотя бы одна 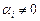(i = 1, 2), а тождество (5) возможно, то функции y₁(x), y₂(x), называются линейно зависимыми.

Пример. 1. y₁ = , y₂ = —линейно независимые функции при .

2. y₁ = , y₂ = — линейно независимые функции.

Теорема. Если y₁, y₂ — какие-либо два линейно независимые частные решения однородного линейного уравнения (4), то его общим решением служит функция y = C₁ y₁ + C₂ y₂ , где C₁, C₂ — произвольные постоянные.