Типовая задача 6. Найти общее решение дифференциального уравнения и частное решение, удовлетворяющее начальному условию .
Найти общее решение дифференциального уравнения 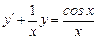 и частное решение, удовлетворяющее начальному условию
и частное решение, удовлетворяющее начальному условию 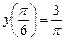 .
.
Решение. Это линейное неоднородное дифференциальное уравнение первого порядка решаем методом Бернулли. Полагаем, что y = u · v, где u, v — некоторые неизвестные пока функции. Тогда y' = u' · v + u · v'. Подставляя в данное уравнение вместо y, y' их указанные значения, получим:
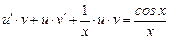
или
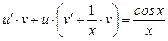 . (9)
. (9)
Выберем функцию 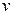 таким образом, чтобы выполнялось равенство
таким образом, чтобы выполнялось равенство 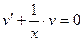 .
.
Отсюда, учитывая, что 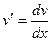 , представим уравнение в виде
, представим уравнение в виде
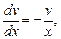
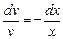 .
.
Интегрируем: 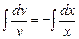 .
.
Отсюда
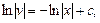
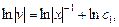 где с = lnc1 ,
где с = lnc1 ,
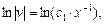
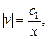
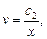 где с2 =
где с2 = 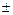 c1 .
c1 .
Пусть с2 = 1. Тогда 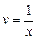 .
.
Подставляя полученное значение функции v в формулу (9),
получим:
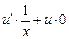 =
= 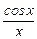 ,
, 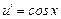 ,
,
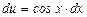 ,
, 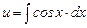 , u = sin x + C.
, u = sin x + C.
Таким образом, 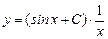 — общее решение данного дифференциального уравнения.
— общее решение данного дифференциального уравнения.
Теперь решаем задачу Коши. Подставляем в формулу общего решения вместо х, у соответственно числа 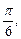
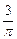 :
:
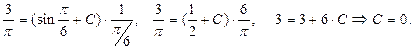
Итак, 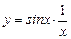 — частное решение данного дифференциального уравнения, удовлетворяющее поставленному начальному условию.
— частное решение данного дифференциального уравнения, удовлетворяющее поставленному начальному условию.
Ответ: 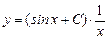 ,
, 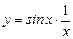 .
.
Дата добавления: 2014-12-02; просмотров: 1211;
