Типовая задача 7. Найти общее решение дифференциального уравнения y'' – 5y' + 4y = = x2 – 1.
Найти общее решение дифференциального уравнения y'' – 5y' + 4y =
= x2 – 1.
Решение. Это линейное неоднородное дифференциальное уравнение второго порядка с постоянными коэффициентами. Решаем однородное уравнение y'' – 5y' + 4y = 0. Для этого составляем характеристическое уравнение k2 – 5k + 4 = 0, откуда k1 = 1, k2 = 4.
Тогда y = C1 · ex + C2 · e4x — общее решение однородного уравнения.
Находим частное решение  неоднородного уравнения. Его будем искать в виде
неоднородного уравнения. Его будем искать в виде 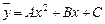 .
.
Тогда 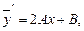
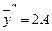 . Подставляя полученные значения
. Подставляя полученные значения  ,
, 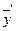 ,
, 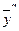 в исходное уравнение, будем иметь:
в исходное уравнение, будем иметь:
2A – 10Ax – 5B + 4Ax2 + 4Bx + 4C = x2 – 1,
или
4Ax2 + (4B – 10A) · x + 2A – 5B + 4C = x2 – 1.
Два многочлена между собой равны тогда и только тогда, когда равны коэффициенты при одинаковых степенях. Отсюда
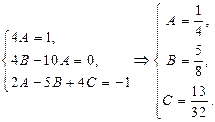
Таким образом, 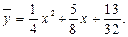
Итак, 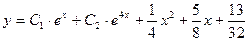 — общее решение данного неоднородного уравнения.
— общее решение данного неоднородного уравнения.
Ответ: 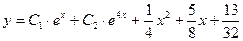 .
.
Дата добавления: 2014-12-02; просмотров: 2397;
