Понятие о дифференциальном уравнении и его решении

Обыкновенным дифференциальным уравнением n-го порядка называется уравнение

= 0,(1)

связывающее независимую переменную, искомую функцию и ее производные вплоть до n-го порядка.

Решением дифференциального уравнения (1) называется такая функция y = , которая при подстановке ее в это уравнение обращает его в тождество.

Общим решением дифференциального уравнения (1) называется такое его решение

y =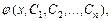

которое является функцией переменной х и п произвольных постоянных C₁, C₂, …, C_n.

Частным решением дифференциального уравнения (1) называется такое его решение, которое получается из общего при некоторых конкретных числовых значениях постоянных C₁, C₂, …, C_n. Процесс нахождения решения дифференциального уравнения называется его интегрированием.

Построенный на плоскости Oxy график решения y = дифференциального уравнения называется интегральной кривой этого уравнения.

К рассмотрению дифференциальных уравнений приводят многие задачи экономики. Например, неоклассическая задача экономического роста приводит к дифференциальному уравнению первого порядка. Непрерывные модели экономики с применением дифференциальных уравнений (независимой переменной является время) достаточно эффективны при исследовании эволюции экономических систем на длительных интервалах времени. Они являются предметом исследования экономической динамики.