Понятие числового знакоположительного ряда

Числовым рядом (или просто рядом)

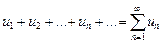(1)

называется бесконечная последовательность чисел u₁, u₂,…, u_n, …, соединенных знаком сложения.

Числа u₁, u₂,…, u_n,… называются членами ряда, u_n — общим членом ряда.

Ряд считается заданным, если известен его общий член u_n = f(n), т. е. задана функция от натурального аргумента.

Рассмотрим суммы конечного числа членов ряда:

S₁ = u₁, S₂ = u₁ + u₂, …, S_n = u₁ + u₂ + …+ u_n .

Сумма S_n первых n членов ряда называется n-й частичной суммой ряда.

Ряд называется сходящимся, если существует конечный предел последовательности его частичных сумм, т. е.

.

Число S называется суммой ряда (1) и записывается в виде

.

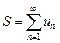Если 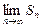не существует или 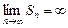, то ряд называется расходящимся. Такой ряд суммы не имеет.