Признаки сходимости
Теорема (необходимый признак сходимости ряда). Если ряд (1) сходится, то его общий член un стремится к нулю при 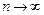 , т. е.
, т. е. 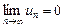 .
.
Для сходимости ряда (1) требование 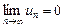 не достаточно.
не достаточно.
Пример. Ряд 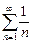 , называемый гармоническим рядом, расходится, хотя и
, называемый гармоническим рядом, расходится, хотя и 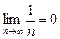 .
.
Следствие (достаточное условие расходимости ряда). Если 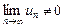 или этот предел не существует, то ряд расходится.
или этот предел не существует, то ряд расходится.
Простейшими примерами числовых рядов являются следующие ряды:
1. Обобщенный гармонический ряд 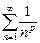 (n
(n  N, p
N, p  R).
R).
Он сходится при p > 1, расходится при p £ 1.
2. Ряд, составленный из членов бесконечной геометрической прогрессии 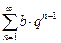 .
.
При |q| ³ 1 он расходится, при |q| < 1 — сходится.
Перечислим некоторые признаки сходимости для числовых рядов с положительными членами.
Признак Даламбера.Если существует предел 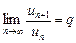 , то:
, то:
1. При 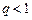 ряд (1) сходится.
ряд (1) сходится.
2. При 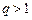 ряд (1) расходится.
ряд (1) расходится.
3. При q = 1 вопрос о сходимости остается открытым.
Признак Коши.Если существует 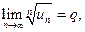 то:
то:
1. При 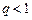 ряд (1) сходится.
ряд (1) сходится.
2. При 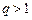 ряд (1) расходится.
ряд (1) расходится.
3. При q = 1 вопрос о сходимости остается открытым.
Признаки сравнения
Пусть даны два ряда
u1 + u2 + … + un + … , (2)
v1 + v2 + … + vn + … . (3)
1. Если un £ vn и ряд (3) сходится, то сходится и ряд (2).
Если ряд (2) расходится, то расходится и ряд (3).
Пример. Так как ряд 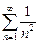 сходится (частный случай при
сходится (частный случай при 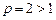 обобщенного гармонического ряда) и
обобщенного гармонического ряда) и 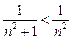 , то сходится и ряд
, то сходится и ряд 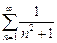 .
.
Пример. Ряд 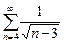 расходится, так как расходится ряд
расходится, так как расходится ряд 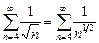 (частный случай при p =
(частный случай при p = 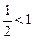 обобщенного гармонического ряда) и
обобщенного гармонического ряда) и 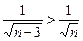 .
.
2. Если существует конечный предел 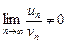 , то ряды (2) и (3) сходятся или расходятся одновременно.
, то ряды (2) и (3) сходятся или расходятся одновременно.
Пример. Ряд 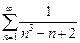 является сходящимся, так как существует сходящийся ряд
является сходящимся, так как существует сходящийся ряд 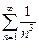 (частный случай при p = 3 > 1 обобщенного гармонического ряда) и конечный предел:
(частный случай при p = 3 > 1 обобщенного гармонического ряда) и конечный предел:
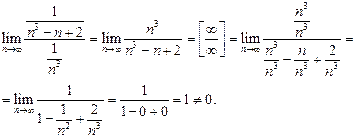
Дата добавления: 2014-12-02; просмотров: 962;
