Типовая задача 2
Найти неопределенные интегралы:
1) 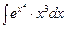 ;
;
2)  ;
;
3) 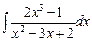 .
.
Результаты проверить дифференцированием.
Решение. 1) Так как 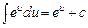 , то, положив u = x4, получим
, то, положив u = x4, получим
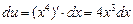 .
.
Отсюда 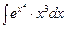 =
= 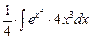 =
= 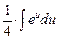 =
= 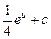 =
=
= 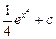 .
.
Проверка: 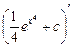 =
= 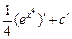 =
= 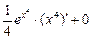 =
= 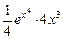 =
=
= 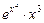 .
.
2) Применим формулу интегрирования по частям:
u = arctg2x  du =
du = 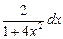 , dv = xdx
, dv = xdx  v =
v = 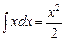 .
.
Тогда 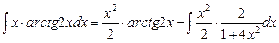 =
= 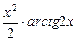 –
–
– 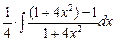 =
= 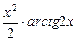 –
– 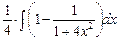 =
= 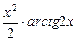 –
–
– 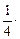
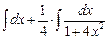 =
= 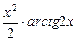 –
– 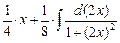 =
= 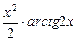 –
–
– 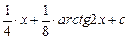 .
.
Проверка: 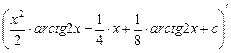 =
= 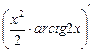 –
–
– 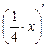 +
+ 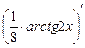 + с' =
+ с' =  +
+ 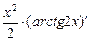 –
– 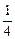 +
+
+ 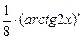 + 0 =
+ 0 = 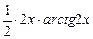 +
+ 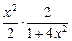 –
– 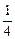 +
+ 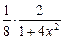 = =
= = 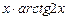 +
+ 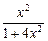 –
– 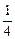 +
+ 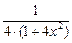 =
= 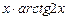 +
+ 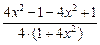 =
=
= 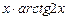 .
.
3) Данная подынтегральная дробь неправильная, поэтому сначала выделим целую часть, поделив числитель на знаменатель:
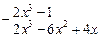
| x2 – 3x + 2 | ||
| 2x + 6 | |||
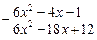
| |||
| 14x – 13 | |||
Итак, 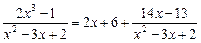 .
.
Отсюда 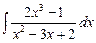 =
= 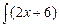 dx +
dx + 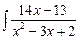 dx = [х2 – 3х + 2 =
dx = [х2 – 3х + 2 =
= (х – 1) · (х – 2)] =  +
+  = I .
= I .
Представим правильную дробь в виде суммы простейших:
 =
= 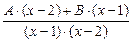 = =
= = 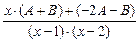 .
.
Избавляясь от знаменателей, получим
14х – 13 = (А + В) · х + (–2А – В).
Приравнивая соответствующие коэффициенты при неизвестных в левой и правой частях равенства, получим систему уравнений
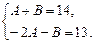

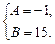
Тогда 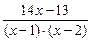 =
= 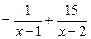 .
.
Итак, 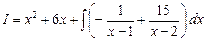 =
= 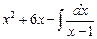 +15·
+15· 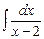 =
=
= 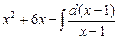 +
+ 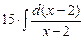 =
=  +
+ 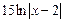 + с.
+ с.
Проверка: 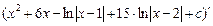 = (х2)' + (6х)' –
= (х2)' + (6х)' –
– (ln |x – 1|)' + (15 · ln|x – 2|)' + c' = 2x + 6 – 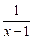 · (x – 1)' +
· (x – 1)' +
+ 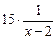 · (x – 2)' + 0 = 2x + 6 –
· (x – 2)' + 0 = 2x + 6 – 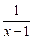 +
+ 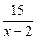 =
=
= 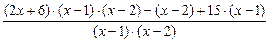 =
=
= 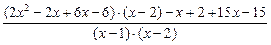 =
=
= 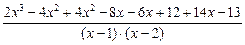 =
= 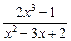 .
.
Ответ: 1) 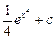 ; 2)
; 2) 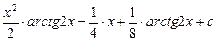 ;
;
3)  +
+ 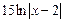 + с.
+ с.
Типовая задача 3
Найти площадь фигуры, заключенной между линиями y = x2 – 7x +
+ 12, y = x – 3.
Решение. Фигура имеет вид, изображенный на рис. 19.
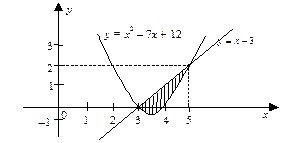
|
| Рис. 19 |
Определим координаты точек пересечения линий. Для этого решим следующую систему уравнений:
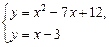

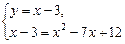

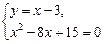



Абсциссы точек пересечения линий — х = 3, х = 5. Следовательно, пределы интегрирования — а = 3, b = 5.
Таким образом, 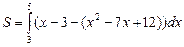 =
= 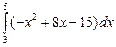 =
=
= 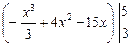 =
= 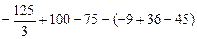 =
= 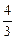 (кв. ед.).
(кв. ед.).
Ответ: 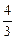 кв. ед.
кв. ед.
3. Задания 4 и 5
по теме «Ряды и их применение
к приближенным вычислениям определенных интегралов»
Дата добавления: 2014-12-02; просмотров: 1001;
