Определенный интеграл и его основные свойства
Пусть на отрезке [a,b] определена функция у = f(x). Разобьем этот отрезок на п частей точками 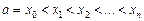 = b. На каждом отрезке [хi–1; xi] возьмем произвольную точку
= b. На каждом отрезке [хi–1; xi] возьмем произвольную точку 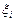 (i = 1, 2,…, п) и составим сумму
(i = 1, 2,…, п) и составим сумму 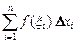 , где
, где 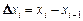 . Сумма
. Сумма 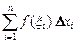 называется интегральной суммой функции f(x) на отрезке [a,b], а ее предел при
называется интегральной суммой функции f(x) на отрезке [a,b], а ее предел при 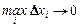 , если он существует и конечен, называется определенным интегралом от функции у = f(x) в пределах от а до b и обозначается следующим образом:
, если он существует и конечен, называется определенным интегралом от функции у = f(x) в пределах от а до b и обозначается следующим образом:
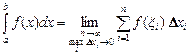 .
.
В этом случае функция у = f(x) называется интегрируемой на отрезке [a,b].
Среди многих экономических интерпретаций определенного интеграла отметим следующую:
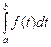 равен объему производства от момента времени t при условии, что f(t) — производительность труда в момент времени t.
равен объему производства от момента времени t при условии, что f(t) — производительность труда в момент времени t.
Определенный интеграл имеет следующие свойства:
1. 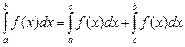 .
.
2. 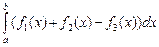 =
= 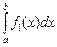 +
+ 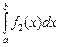 –
– 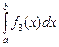 .
.
3. 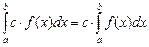 .
.
Дата добавления: 2014-12-02; просмотров: 997;
