Интегрирование простейших рациональных дробей
Интегрирование проводят в зависимости от типа простейшей рациональной дроби.
1. 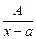 (А, а — постоянные действительные числа) — простейшая рациональная дробь первого типа.
(А, а — постоянные действительные числа) — простейшая рациональная дробь первого типа.
Пример. 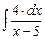 =
= 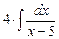 =
= 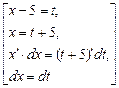 =
= 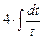 = =
= = 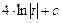 =
= 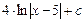 .
.
2. 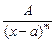 (А, а, т — постоянные числа,
(А, а, т — постоянные числа, 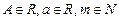 ,
, 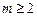 ) — простейшая рациональная дробь второго типа.
) — простейшая рациональная дробь второго типа.
Пример. 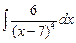 =
= 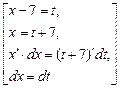 =
= 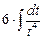 =
= 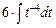 =
=
= 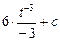 =
= 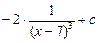 =
= 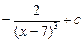 .
.
3. 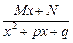 (М, N, p, q — постоянные числа, М, N, p, q
(М, N, p, q — постоянные числа, М, N, p, q 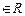 , х2 + рх + q не имеет действительных корней) — простейшая рациональная дробь третьего типа.
, х2 + рх + q не имеет действительных корней) — простейшая рациональная дробь третьего типа.
Пример. 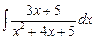 =
= 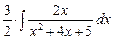 +
+ 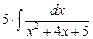 =
=
= 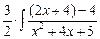 dx +
dx + 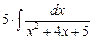 =
= 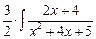 dx –
dx – 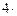
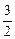 ·
·
· 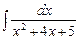 + 5 ·
+ 5 · 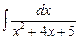 =
= 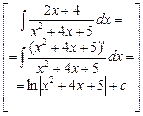 =
=
= 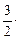
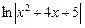 –
– 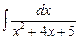 =
= 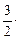
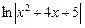 –
– 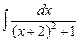 =
=
=[d(x + 2) = (x + 2)'dx = dx] = 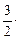
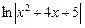 –
– 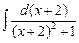 =
= 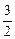 ·
·
· 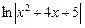 – arctg(x + 2) + c.
– arctg(x + 2) + c.
4. 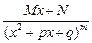 (М, N, р, q — постоянные числа, М, N, р, q
(М, N, р, q — постоянные числа, М, N, р, q 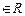 ,
, 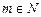 ,
, 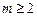 ; х2 + рх + q не имеет действительных корней) — простейшая рациональная дробь четвертого типа.
; х2 + рх + q не имеет действительных корней) — простейшая рациональная дробь четвертого типа.
Интеграл от этой дроби считается с помощью рекуррентных формул, позволяющих уменьшить число т до 1.
Дата добавления: 2014-12-02; просмотров: 826;
