Полный дифференциал

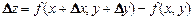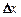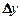Полным приращением функции z = f(x,y) в точке М(х,у)называется разность , где , — произвольные приращения аргументов.

Функция z = f(x,y) называется дифференцируемой в точке (x,y), если ее полное приращение может быть представлено в виде

,

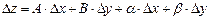где А и В, не зависящие от 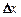и 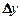, — постоянные; 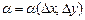, 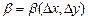— бесконечно малые при 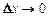, 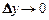функции, равные нулю при 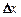= = 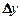0.

Полным дифференциалом функции z = f(x, y) называется главная часть полного приращения 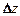, линейная относительно приращений аргументов 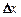, , 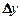т. е. .

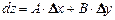Для независимых переменных х, у полагают, что , .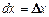

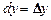Поэтому полный дифференциал функции z = f(x, y) вычисляется по формуле

.

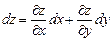Пример. Для функции z = x²y получим:

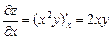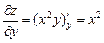, , dz = 2xy dx + x²dy.

Вопросы для самопроверки

Что вы понимаете под функцией нескольких переменных?

Какие вы знаете примеры функций нескольких переменных?

Что называется частной производной функции двух переменных?

Как вычислить полное приращение функции z = f(x, y) в произвольной точке?

Какая функция называется дифференцируемой в точке (x, y)?

Что называется полным дифференциалом функции z = f(x, y)?

По какой формуле вычисляется полный дифференциал функции двух переменных?

Типовая задача 1

Показать, что функция и = у · ln(x² – y²) удовлетворяет соотношению .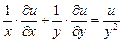

Решение. Находим частные производные:

= = = ,

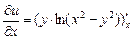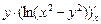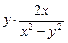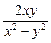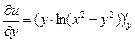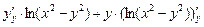= = ln(x² –
– y²) + 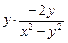= ln(x² – y²) – .

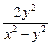Подставляем полученные значения в соотношение:

= +
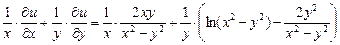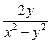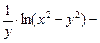
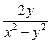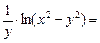
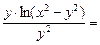
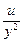+ = , что и требовалось показать.

2. Задания 2 и 3
по теме «Неопределенный интеграл,
определенный интеграл и его применение
для вычисления площади фигуры»