Понятие неопределенного интеграла. Функция F(x) называется первообразной для функции f(x) на некотором промежутке Х, если для любого элемента выполняется равенство F'(x) = f(x).
Функция F(x) называется первообразной для функции f(x) на некотором промежутке Х, если для любого элемента 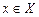 выполняется равенство F'(x) = f(x).
выполняется равенство F'(x) = f(x).
Если F(x) — одна из первообразных для функции f(x) на промежутке Х, то всякую другую первообразную Ф(х) на промежутке Х можно представить в виде Ф(х) = F(x) + с, где с — постоянная величина.
Неопределенным интегралом от функции f(x) называется множество всех ее первообразных, т. е. 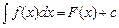 .
.
При этом f(x) — подынтегральная функция, f(x)dx — подынтегральное выражение, 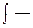 знак неопределенного интеграла, х —
знак неопределенного интеграла, х —
переменная интегрирования.
Операция нахождения неопределенного интеграла от функции называется интегрированием этой функции.
Свойства неопределенного интеграла:
1. 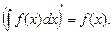
2. 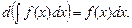
3. 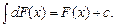
4. 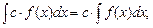 где с — постоянная величина.
где с — постоянная величина.
5. 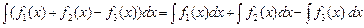 .
.
6. Если 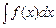 = F(x) + c и
= F(x) + c и 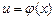 — дифференцируемая функция, то
— дифференцируемая функция, то 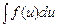 = F(и) + c.
= F(и) + c.
Таблица основных неопределенных интегралов:
1. 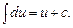
2. 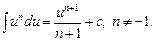
3. 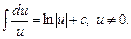
4. 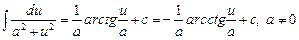 .
.
5. 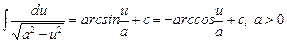 .
.
6. 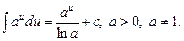
7. 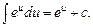
8. 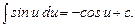
9. 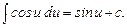
10. 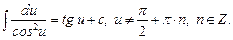
11. 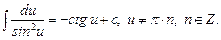
12. 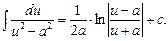
13. 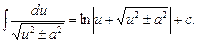
14. 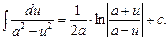
15. 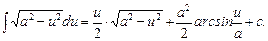
16. 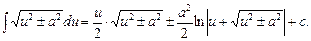
Дата добавления: 2014-12-02; просмотров: 967;
