Знакопеременные ряды. Если знаки членов ряда (1) строго чередуются, то ряд называется знакочередующимся (знакопеременным).

Если знаки членов ряда (1) строго чередуются, то ряд называется знакочередующимся (знакопеременным).

Знакопеременный ряд 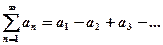(2) называется абсолютно сходящимся если ряд,

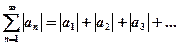(3), составленный из абсолютных значений его членов сходится.

Знакопеременный сходящийся ряд (2) называется условно сходящимся, если ряд (3) расходится.

Всякий абсолютно сходящийся ряд есть ряд сходящийся.ъ

Признак Лейбница

Знакочередующийся ряд 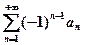, 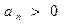сходится, если его члены убывают по абсолютному значению, стремясь к нулю, т.е. если 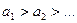и .

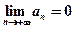Пример 10. Доказать сходимость ряда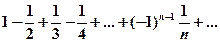

Решение :

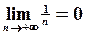, . Условия признака Лейбница выполняются, следовательно ряд сходится.