Градиент. Производная по направлению

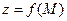Скалярным полем называется плоская или пространственная область, с каждой точкой которой связано определенное значение некоторой физической величины . Задание поля скалярной величины 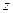равносильно заданию скалярной (числовой) функции .

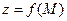Линией уровня скалярного поля называется совокупность точек плоскости, в которых функция этого поля имеет одинаковые значения ( 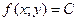, где ).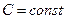

Градиентом функции 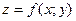называется вектор

= .

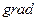
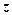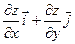Направлениевектора 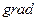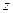в каждой точке 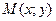совпадает с направлением нормали к поверхности (линии) уровня, проходящей через эту точку.

Производная функции 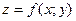в точке 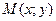в направлении вектора 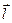, образующего с осями координат углы 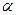и , вычисляется по формуле

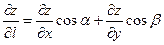
Пример 15. Найти градиент и производную функции 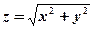в точке М(3,4₎ в направлении вектора l, составляющего угол 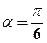с положительным направлением оси Ох.

Решение. Найдем частные производные функции в точке М:

.

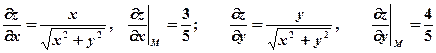Тогда градиент будет равен: .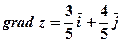

Найдем направляющие косинусы: 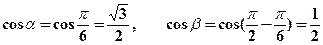. Тогда производная по направлению будет равна

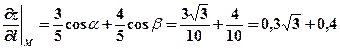
Варианты индивидуальных заданий