Функции нескольких переменных
Пусть задано множество 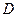 упорядоченных пар чисел
упорядоченных пар чисел  . Соответствие
. Соответствие 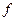 , которое каждой паре чисел
, которое каждой паре чисел 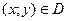 сопоставляет одно и только одно число
сопоставляет одно и только одно число 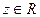 , называется функцией двух переменных, определенной на множестве
, называется функцией двух переменных, определенной на множестве 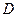 со значениями в
со значениями в 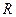 , и записывается в виде
, и записывается в виде 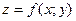 .
.
Частной производной функции нескольких переменных называется производная функции одной из этих переменных при условии постоянства значений остальных переменных. Обозначения частных производных: 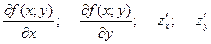 .
.
Частные производные 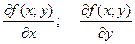 называют частными производными первого прядка. Их можно рассматривать как функции от
называют частными производными первого прядка. Их можно рассматривать как функции от 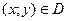 . Эти функции также могут иметь частные производные, которые называются частными производными второго порядка. Они определяются и обозначаются следующим образом:
. Эти функции также могут иметь частные производные, которые называются частными производными второго порядка. Они определяются и обозначаются следующим образом:


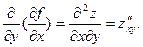
Частные производные второго или более высокого порядка, взятые по различным переменным, называются смешанными частными производными.
Теорема. Если частные производные непрерывны, то смешанные производные одного порядка, отличающиеся лишь порядком дифференцирования, равны между собой.
В частности, для 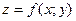 имеем:
имеем: 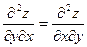
Пример 13. Найти производные первого порядка и смешанную производную второго порядка функции 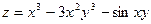 .
.
Решение. При нахождении частной производной по  полагаем
полагаем 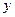 постоянной:
постоянной: 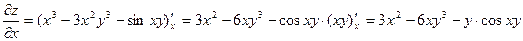 . При нахождении частной производной по
. При нахождении частной производной по 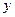 полагаем
полагаем  постоянной:
постоянной: 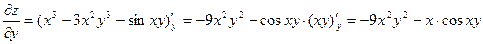 .
.  .
.
Дата добавления: 2014-12-08; просмотров: 1115;
