Знакоположительные ряды

Для числовых рядов с положительными членами , при исследовании сходимости используются следующие достаточные признаки.

Интегральный признак Коши

Ряд с положительными убывающими членами 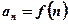сходится или расходится в зависимости от того, сходится или расходится несобственный интеграл 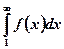, где 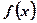- непрерывная убывающая функция.

Нижним пределом несобственного интеграла может быть любое число 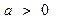из области определения 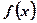. Этим признаком можно пользоваться, когда выражение общего члена 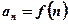имеет смысл не только для целых положительных значений n но и для всех n, больших некоторого положительного числа т.

Пример 7.

Исследовать сходимость гармонического ряда:

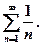
Решение:

Заменяем в выражении общего члена 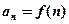номер n непрерывной переменно 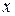и убеждаемся, что является непрерывной убывающей функции при 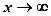Вычислим несобственный интеграл

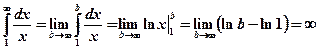.Несобственный интеграл расходится, следовательно, расходится и гармонический ряд.

Признак Даламбера

Если 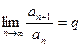,то при q<1ряд сходится, а при q>1расходится. При q=1 вопрос о сходимости ряда остается нерешенным.

Пример 8.

Исследовать на сходимость ряд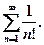

Решение:

.

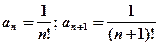Применим признак Даламбера:

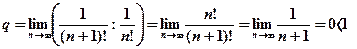.Так как 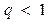то по признаку Даламбера исследуемый ряд сходится.

Признак сравнения

Пусть даны два ряда с положительными членами

… (а)

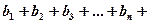… (б)

если начиная с некоторого номера n:

1) 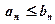и ряд (б) сходится, то и ряд (а) также сходится;

2) 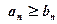и ряд (б) расходится, то и ряд(а) также расходится.

При использовании этого признака исследуемый ряд часто сравнивается либо с бесконечной геометрической прогрессией , которая при 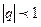сходится, а при 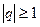расходится, либо с гармоническим рядом.

Пример 9

Исследовать ряд на сходимость с помощью признака сравнения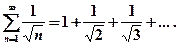

Решение:

Каждый член 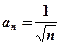данного ряда, начиная со второго, больше соответствующего члена гармонического ряда: 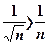, и, так как гармонический ряд расходится, то, согласно признаку сравнения, исходный ряд также расходится.