Введение. 1. Пискунов Н.С. Дифференциальное и интегральное исчисления: Учеб

1. Пискунов Н.С. Дифференциальное и интегральное исчисления: Учеб. пособие: В 2-х т. – Изд. стереотип. – М.: Интегралпресс. Т. 1. – 1991. – 416 с.

2. Шипачев В.С, Высшая математика: Учеб./под ред. А.Н. Тихонова. – 2-е изд. стереотип. – М.: Высш. шк., 1990. – 479 с.

3. Письменный Д.Т. Конспект лекций по высшей математике. I, IIч.. –М.:Рольф, 2002. – 288с.

4. Зайцев И.А. Высшая математика: Учеб. – М.: Высш. шк., 1991. – 400с.

5. Берман Г.Н. Сборник задач по курсу математического анализа: Учеб. пособие. – 20-е изд. – М.: Наука, 1985. – 416 с.

6. Данко П.Е. и др. Высшая математика в упражнениях и задачах: В 2ч. – М.: Высш. шк. т.1. – 1999. – 304 с.

7. Шипачев В.С. Задачник по высшей математике: Учеб. пособие. – 2-е изд., испр. – М.: Высш. шк., 2000. – 304 с.

Введение

Целью настоящих методических указаний является помощь студентам – заочникам в выполнении контрольной работы №3.

Перед выполнением контрольной работы студент должен изучить соответствующие разделы рекомендуемой литературы и воспользоваться решениями типовых примеров, содержащихся в настоящих методических указаниях.

Номер варианта по каждому заданию студент выбирает по формуле ,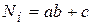

где 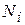- номер варианта,

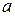-номер задания,

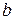-предпоследняя цифра шифра студента,

-последняя цифра шифра.

Пример.

Пусть шифр студента 1235, тогда:

номер варианта первого задания: = ;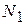

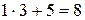номер варианта второго задания: ;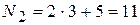

номер варианта третьего задания: ;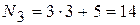

номер варианта четвертого задания: .

Таким образом, студент, имеющий шифр 1235 должен решать задачу №8 в первом задании, №11 – во втором, №14 – в третьем, №17 – в четвертом.

Если итоговая число по формуле получится больше 20, то для определения варианта от полученного числа отнимают 20.

Пример.

Пусть шифр студента 1298.

Номер варианта второго задания: 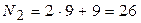. Промежуток 26-20=6. Таким образом, во втором задании студент решает задачу варианта №6.

Основная цель инженера – исследователя, изучающего какой- либо физический или технический процесс, заключается в выявлении его закономерностей, в получении аналитического выражения функциональной зависимости между переменными параметрами этого процесса.

Большинство подобных задач сводится к решению уравнений, содержащих производные или дифференциалы неизвестных функций.

Ряды

Числовым рядом называется выражение

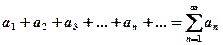(1)

Ряд называется сходящимся, если сумма n первых его членов 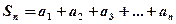имеет предел при 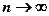. Иначе ряд называется расходящимся. Ряд может сходиться лишь при условии, когда общий член ряда 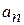стремится к нулю при 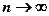: (Это необходимый, но не достаточный признак сходимости для всякого ряда).

Если же , то ряд расходится. (Это достаточный признак расходимости всякого ряда).

Пример 5. Дан ряд 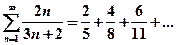. Проверить выполнение необходимого признака.

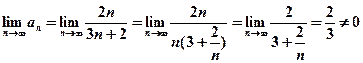
Необходимый признак не выполняется. Следовательно, ряд расходится.

Пример 6.

Дан гармонический ряд 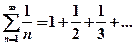: Найдем для него .

Для него необходимый признак выполняется, вследствие чего он может быть или сходящимся или расходящимся, что можно установить дополнительным исследованием. (Смотри ниже).