Логарифмическая производная

Если производная от логарифмов – это такая сладкая музыка, то возникает вопрос, а нельзя ли в некоторых случаях организовать логарифм искусственно? Можно! И даже нужно.

Пример 11

Найти производную функции

Похожие примеры мы недавно рассмотрели. Что делать? Можно последовательно применить правило дифференцирования частного, а потом правило дифференцирования произведения. Недостаток способа состоит в том, что получится огромная трехэтажная дробь, с которой совсем не хочется иметь дела.

Но в теории и практике есть такая замечательная вещь, как логарифмическая производная. Логарифмы можно организовать искусственно, «навесив» их на обе части:

Теперь нужно максимально «развалить» логарифм правой части (формулы перед глазами?). Я распишу этот процесс очень подробно:

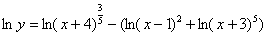
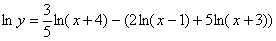
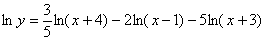
Собственно приступаем к дифференцированию.
Заключаем под штрих обе части:

Производная правой части достаточно простая, её я комментировать не буду, поскольку если вы читаете этот текст, то должны уверенно с ней справиться.

Как быть с левой частью?

В левой части у нас сложная функция. Предвижу вопрос: «Почему, там же одна буковка «игрек» под логарифмом?».

Дело в том, что эта «одна буковка игрек» – САМА ПО СЕБЕ ЯВЛЯЕТСЯ ФУНКЦИЕЙ (если не очень понятно, обратитесь к статье Производная от функции, заданной неявно). Поэтому логарифм – это внешняя функция, а «игрек» – внутренняя функция. И мы используем правило дифференцирования сложной функции :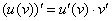

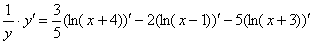
В левой части как по мановению волшебной палочки у нас «нарисовалась» производная 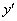. Далее по правилу пропорции перекидываем «игрек» из знаменателя левой части наверх правой части:

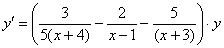
А теперь вспоминаем, о каком таком «игреке»-функции мы рассуждали при дифференцировании? Смотрим на условие:

Окончательный ответ:

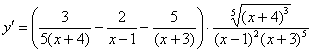
Пример 12

Найти производную функции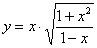

Это пример для самостоятельного решения. Образец оформления примера данного типа в конце урока.

С помощью логарифмической производной можно было решить любой из примеров №№4-7, другое дело, что там функции проще, и, может быть, использование логарифмической производной не слишком-то и оправдано.