Правила дифференцирования. Производная сложной функции.

Основные правила дифференцирования:

1. Производная постоянной равна нулю, т.е. С¢=0.

2. Производная аргумента равна 1, т.е. х¢=1.

3. Производная алгебраической суммы конечного числа дифференцируемых функций равна такой же сумме производных этих функций, т.е. (u + v)¢ = u¢ + v¢.

4. Производная произведения двух дифференцируемых функций вычисляется по формуле: (u v)¢ = u¢ v + u v¢.

Следствие. Постоянный множитель можно выносить за знак производной: (Сu)¢ = Cu¢.

5. Производная частного двух дифференцируемых функций может быть найдена по формуле:

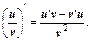
Теорема. Если у=f(u) и u =j(x) – дифференцируемые функции от своих аргументов, то производная сложной функции существует и равна произведению данной функции по промежуточному аргументу и умноженной на производную самого промежуточного аргумента по независимой переменной х, т.е у¢ = ¦¢(u)u¢.

Вычисление производных мы будем вести не непосредственно, исходя из определения производной, а по формулам приведенным в таблице 1 Приложения 1.

Пример 3. Найти производную функции у = х⁴.

Р е ш е н и е. Учитывая замечание, которое только что сделано по формуле 8 из таблицы производных, пологая в ней u = х, имеем: в этом примере показатель степени n = 4, а потому у¢ = 4 х³.

Пример 4. Найти производную функции у = sin х⁴.

Р е ш е н и е. Данная функция сложная. Введя обозначение u = х⁴, получим у =sin u . Теперь по формуле 9 из таблицы производных находим

у¢ = сos u × 4х³ = сos х⁴ × 4х³.