Определение производной.
Пусть дана функция у = ¦(х). Рассмотрим два значения ее аргумента: исходное – х0 и новое – х.
Разность Dх = х - х0 называется приращением аргумента х в точке х0.
Разность Dу = у – у0 =¦(х) - ¦(х0) называется приращением функции у = ¦(х) в точке х0.
Так как х = х0+Dх, а у = у0+Dу, то Dу = ¦( х0+Dх ) - ¦( х ).
Пример 1. Найти приращение функции у = х2 в точке х0.
Р е ш е н ие. Dу = ¦( х0+Dх ) - ¦( х ) = [х0+Dх]2 – [х0]2 = [(х0)2+2xDх + + (Dх)2] – [х0]2 = 2 х0 Dх + (Dх)2.
Пусть функция у = ¦(х) определена на промежутке Х.Возьмем точку хÎХ. Дадим значению х приращение Dх¹0, тогда функция получит приращение Dу = ¦( х+Dх ) - ¦( х ). Производной функции у = ¦(х) называется предел отношения приращения функции Dу к приращению аргумента Dх при стремлении Dх к нулю.
Производная функции у = ¦(х) обозначается символом ¦¢( х).
Если функция в точке х0 имеет конечную производную, то функция называется дифференцируемой в этой точке. Производная функции у = ¦(х) в точке х0 является значением функции ¦¢( х) в точке х0.
Функция, дифференцируемая во всех точках промежутка Х, называется дифференцируемой на этом промежутке.
Пример 2. Найти производную функции у = х2.
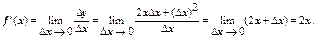 |
Р е ш е н и е. В примере 1 мы уже нашли Dу = 2 хDх + (Dх)2. Тогда
Нахождение производной функции называется дифференцированием этой функции.
Дата добавления: 2014-12-16; просмотров: 1134;
