Непрерывность функции.
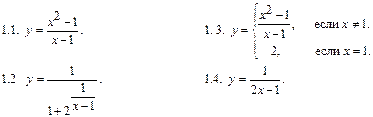 |
1) Какие из данных функций являются непрерывными в точке х = 1. В случае нарушения непрерывности установить характер точки разрыва:
2) Исследовать непрерывность функции в точке х=0
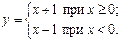
3) Исследовать непрерывность функции в точке х=0
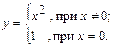
4) Определить, является ли функция непрерывной; если нет, то выяснить характер точки разрыва:
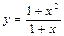 .
.
5) Исследовать на непрерывность функцию
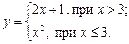
6) Определить, является ли функция непрерывной; если нет, то выяснить характер точки разрыва:
y = (cos 5x)/x.
7) Определить, является ли функция непрерывной; если нет, то выяснить характер точки разрыва:
y = (2x+1)/x2.
8) Определить, является ли функция непрерывной в точке х = 1. В случае нарушения непрерывности установить характер точки разрыва:
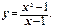
9) Определить, является ли функция непрерывной в точке х = 1. В случае нарушения непрерывности установить характер точки разрыва:
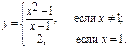
10) Определить является ли функция непрерывной в точке х = 1. В случае нарушения непрерывности установить характер точки разрыва:
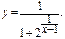
11) Определить, является ли функция непрерывной в точке х = 1. В случае нарушения непрерывности установить характер точки разрыва:
Дата добавления: 2014-12-16; просмотров: 1915;
