Непрерывность функции. Определение 1.Функция ¦(х) называется непрерывной в точке х0, если она удовлетворяет следующим трем условиям: 1) определена в точке х0
 |
Определение 1.Функция ¦(х) называется непрерывной в точке х0, если она удовлетворяет следующим трем условиям: 1) определена в точке х0 (т.е. существует ¦(х0)); 2) имеет конечный предел функции при х ® х0; 3) этот предел равен значению функции в этой точке , т.е.
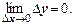 |
Определение 2. Функция у =¦(х) называется непрерывной в точке х0, если она определена в этой точке и бесконечно малому приращению аргумента соответствует бесконечно малое приращение функции:
Пример 1. Исследовать непрерывность заданных функций:
а) ¦(х) = 3х2 + 2х + 1;
б) ¦(х) = (3х2 + 2х + 1)/(х - 1).
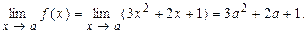 |
Р е ш е н и е. а) Заданная функция определена на бесконечном интервале (-¥, +¥). Возьмем из этого интервала произвольное значение х =а. На основании известных теорем о пределе функции можем написать
Но и ¦(а) = 3а2 + 2а + 1 и, таким образом, у нас выполнено соотношение (5), а это и означает, что рассматриваемая функция непрерывна при х = а. Учитывая, что а – произвольное число интервала, мы заключаем, что данная функция непрерывна при любом значении х, т.е. на бесконечном интервале (-¥, +¥);
б) Эта дробно-рациональная функция определена для всех значений х, кроме тех, которые знаменатель обращают в нуль. Заданная функция непрерывна всюду, кроме значения х =1. О непрерывности в этой точке не может быть и речи, так как она не принадлежит области определения функции.
Теорема.Сумма, разность, произведение и частное двух функций непрерывных в одной и той же точке а, есть функция непрерывная в той же точке, причем в случае частного предполагается, что функция делитель не обращается в нуль при х = а. (Теорема остается верной для суммы и произведения любого конечного числа функций).
Функция у = ¦(х) называется непрерывной на промежутке Х, если она непрерывна в каждой точке этого промежутка. Доказано, что все элементарные функции непрерывны в области их определения.
Дата добавления: 2014-12-16; просмотров: 1046;
