Связь между бесконечно малыми и бесконечно большими величинами.
Теорема. Если функция a(х) является бесконечно малой величиной при х ® х0 или при х ® ¥, то функция f (x)=1/a(х) есть величина бесконечно большая при х ® х0 или при х ® ¥. И обратно, если функция f (x) есть величина бесконечно большая при х ® х0 или при х ® ¥, то функцияa(х) = 1/f(x) является бесконечно малой величиной при х ® х0 или при х ® ¥.
Например, функция f(x) = tgx есть бесконечно большая величина при х ® p¤2, а функция a(х) = 1 / tg x = ctg x является бесконечно малой величиной при х ® p¤2.
При отыскании предела целой рациональной функции можно в аналитическом выражении функции заменить аргумент его предельным значением, т.е. если
 |
Р(х) = а0хn + a1x n-1 + a2xn-2 +…+an-1x +an, то
Пример 1. Найти предел:
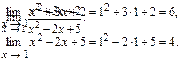 |
Р е ш е н и е. Функции, стоящие в числителе и знаменателе данной дроби, являются целыми рациональными функциями. Для отыскания их пределов применима формула (4). Заменим в аналитическом выражении функции значение х его предельным значением и получим:
Используя свойство предела дроби, получим:
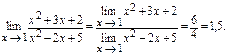 |
Дата добавления: 2014-12-16; просмотров: 1477;
