Предел числовой последовательности.
Если по некоторому закону каждому натуральному числу n поставлено в соответствие вполне определенное число аn, то говорят, что задана числовая последовательность { аn }: a1 , a2 , a3 , ..., an , ... .
Другими словами, числовая последовательность – это функция натурального аргумента: аn = f(n). Числа a1 , a2 , a3 , ..., an называются членами последовательности, а число аn – общим или n-м членом данной последовательности.
Последовательность считается заданной, если дан способ вычисления любого ее члена по известному номеру.
Пример 1. Написать первые пять членов последовательности, если ее общий член аn =n (n+1).
Р е ш е н и е. Вычисляя значение произведения n (n+1) при значениях n, равных 1,2, 3, 4, 5, получим: a1 =2, a2 =6, a3=12, a4=20, a5=30.
Число А называется пределом числовой последовательности { аn }, если для любого, даже сколь угодно малого положительного числа e, найдется такой номер N (зависящий от e), что для всех членов последовательности с номерами n>N верно неравенство
| аn – А |<e (1)
Это неравенство равносильно таким двум неравенствам:
А - e< аn < А + e.
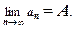 |
Предел числовой последовательности обозначается:
Последовательность, имеющая предел, называется сходящейся, в противном случае – расходящейся.
Дата добавления: 2014-12-16; просмотров: 957;
