Раскрытие неопределенностей при вычислении пределов
I.Неопределённость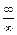 раскрывается:
раскрывается:
1. Делением числителя и знаменателя на наивысшую степень.
 |
Пример 1.
2. Использованием правила Лопиталя (предел отношения функций равен пределу отношения производных этих функций).
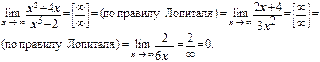 |
Пример 2.
3. 
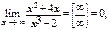 |
Пример 3.
так как степень числителя больше степени знаменателя.
II. Неопределённость  сводится к неопределенности
сводится к неопределенности 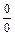 или
или 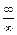 в результате:
в результате:
1. Приведения дроби к общему знаменателю.
2. Перенесения иррациональности в знаменатель.
III. Неопределённость 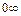 сводится к
сводится к 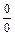 или
или 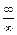 по правилу:
по правилу:
 |
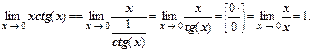 |
Пример 4.
IV.Неопределённость 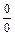 раскрывается по следующему алгоритму:
раскрывается по следующему алгоритму:
a)
1.Числитель и знаменатель приравнять к нулю.
2. Решить полученные уравнения.
3. Числитель и знаменатель разложить на множители.
4. Сократить на общий множитель.
Пример 5.
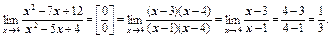
б) При наличии иррациональности:
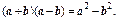 1.Числитель и знаменатель умножить на выражение, сопряженное данному.
1.Числитель и знаменатель умножить на выражение, сопряженное данному.
2. Применить формулу
3. Числитель и знаменатель сократить на общий множитель.
Пример 6.
Р е ш е н и е. Используя правило раскрытия неопределенности 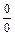 при наличии иррациональности, умножим числитель и знаменатель на сопряженное выражение
при наличии иррациональности, умножим числитель и знаменатель на сопряженное выражение  и применим формулу
и применим формулу 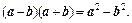

Применение эквивалентных б.м. при раскрытии неопределенности 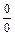
Известно, что для малых х (х→0) имеет место:
sin x ~ x;
tg x ~ x;
arcsin x ~ x;
arctg x ~ x;
ex-1 ~ x;
ln (1+x) ~ x;
ax-1 ~ xlna.
Пример 7.
Найти 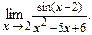
Р е ш е н и е. Функция (x-2) является бесконечно малой величиной при х→2, поэтому sin(х-2)~ х-2.
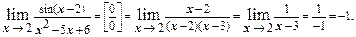
Дата добавления: 2014-12-16; просмотров: 1923;
