Асимптоты графика функции.
Асимптотой графика функции у =¦(х) называется прямая, обладающая таким свойством, что расстояние от переменной точки на графике до этой прямой стремится к нулю при неограниченном удалении этой точки по графику от начала координат.
Нахождение асимптот графика основано на следующих утверждениях.
Теорема 1. Пусть функция у=¦( х) определена в некоторой окрестности точки х0 (исключая, возможно, саму эту точку) и хотя бы один из пределов функции при х® х0 – 0 (слева) или при х® х0 + 0 (справа) – равен бесконечности, тогда прямая при х = х0 является вертикальной асимптотой графика функция у =¦( х).
Замечание. Вертикальные асимптоты следует искать в точках разрыва функции у = ¦( х) или на концах её области определения (а, b), если а и b – конечные числа.
Теорема 2. Пусть функция у=¦(х) определена при достаточно больших х и существует конечный предел функции при х ® ¥ и он равен числу b. Тогда прямая у=b есть горизонтальная асимптота графика функции у =¦( х).
Замечание. Если конечен лишь один из пределов слева или справа, то функция имеет лишь левостороннюю или правостороннюю асимптоту.
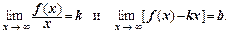 |
Теорема 3. Пусть функция у=¦(х) определена при достаточно больших х и существует конечные пределы:
Тогда прямая у = kx + b является наклонной асимптотой.
Пример 4. Найти асимптоты графика функции у = (х+1)/x.
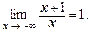 |
Р е ш е н и е. Определяем вертикальную асимптоту по теореме 1 находим точки разрыва функции и выбираем те значения х0, вблизи (слева или справа) которых ¦( х) неограниченно возрастает. Таким значением будет х0 = 0. Вертикальная асимптота имеет уравнение х = 0, т.е. это ось Оу. Находим горизонтальные асимптоты по теореме 2:
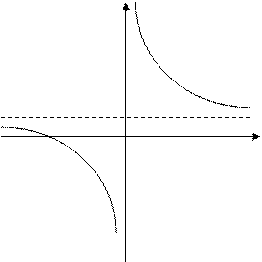
Функция имеет единственную горизонтальную асимптоту у = 1 (рис. 4).
 |
у
0 х
Рис. 4
Дата добавления: 2014-12-16; просмотров: 1691;
