Линейные дифференциальные уравнения с постоянными коэффициентами

Неоднородное уравнение с постоянными коэффициентами

(11)

можно решить с помощью метода неопределенных коэффициентов.

I. Т.к. уравнение (11) неоднородное, его общее решение будет состоять из суммы общего однородного и частного неоднородного уравнений, т.е.

.

Составляем соответствующее однородное уравнение

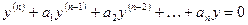(12)

Его характеристическое уравнение

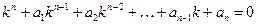(13)

структура фундаментальной системы решений зависит от вида корней характеристического уравнения (13).

Различают 3 случая.

а). Все корни характеристического уравнения (13) различны и вещественны. Обозначим их . Фундаментальная система решений:

,

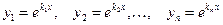а общее решение имеет вид:

.

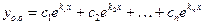б). Все корни характеристического уравнения (13) различны, но среди них имеются комплексные. Пусть 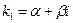— комплексный корень уравнения (13). Тогда 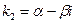— тоже является корнем этого уравнения. Этим корням соответствуют два линейно независимых частных решения:

.

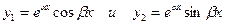Есл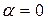и и 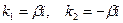то частные решения будут иметь вид

.

Написав линейно независимые частные решения, соответствующие другим сопряженным парам комплексных корней и всем вещественным корням и составив линейную комбинацию из этих решений с произвольными постоянными коэффициентами, получим обще решение уравнения (12).

в). Среди корней характеристического уравнения имеются кратные. Пусть k₁ вещественный r-кратный корень. Тогда ему соответствуют r линейно независимых частных решений вида:

.

Если 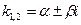— комплексные корни уравнения (13) кратности r, то им соответствует 2r линейно независимых частных решений вида:

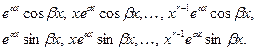
Написав линейно независимые частные решения указанного вида, соответствующие всем простым и кратным вещественным корням, а также сопряженным парам простых и кратных комплексных корней, получим фундаментальную систему решений.

II.По виду правой части уравнения (11) подбирают частное решение неоднородного уравнения.

Возможны случаи.

1). 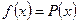, где P(x) – многочлен от x степени n.

а). Если число 0 не является корнем характеристического уравнения (13), то частное решение неоднородного уравнения (11) можно найти в виде 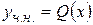, где Q(x) – многочлен от x той же степени n, что и P(x) в общем, виде (т.е. с неопределенными коэффициентами).

Например,

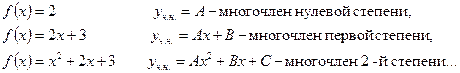
б). Если же 0-корень характеристического уравнения кратности r, то

.

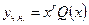2). .

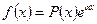а). Если число α не является корнем характеристического уравнения (13), то

.

3) 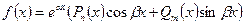, где — многочлены степени m и n соответственно (один из многочленов может быть тождественно равен нулю);

а) если 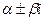не является корнем уравнения (13), то

,

где - многочлены степени .

б) если 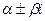является корнем характеристического уравнения кратности r, то

.

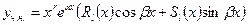4) 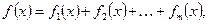где 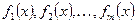— функции вида, рассмотренного 1), 2), 3). Если 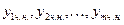являются частными решениями, которые соответствуют функциям 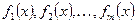, то

.

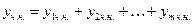Пример. Найти общее решение дифференциального уравнения

.

Решение. Это неоднородное дифференциальное уравнение 3-го порядка, которое не содержит искомой функции y. Составим соответствующее однородное уравнение

.

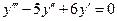Характеристическое уравнение имеет корни: 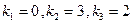(случай Iа). Частные решения однородного уравнения:

.

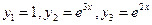Соответственно обще однородного .

Теперь рассмотрим правую часть исходного уравнения: — многочлен второй степени (случай II1). По его виду составим частное решение неоднородного уравнения: .

Множитель x появляется исходя из того, что x=0 является корнем характеристического уравнения. Находя и подставляя найденное в исходное уравнение, получим

.

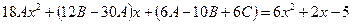Сравнивая коэффициенты при одинаковых степенях, получим систему

,

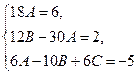из которой A=1/3, B=1, C=1/2. Подставляя эти значения в общий вид частного решения, получим

.

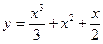Учитывая, что общее решение неоднородного уравнения есть сумма общего однородного и частного неоднородного, имеем

.

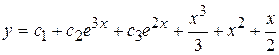Вопросы для самопроверки

1. Дайте определение дифференциального уравнения первого порядка и его общего и частного решения (интеграла). Сформулируйте задачу Коши для дифференциального уравнения первого порядка и укажите ее геометрический смысл.

2. Дайте геометрическое истолкование дифференциального уравнения первого порядка, выясните геометрический смысл общего и частного решений.

3. Сформулируйте теорему о существовании и единственности решения дифференциального уравнения первого порядка.

4. Дайте определение дифференциального уравнения с разделяющимися переменными. Изложите метод нахождения его общего решения. Приведите примеры.

5. Дайте определение однородного дифференциального уравнения первого порядка. Изложите метод нахождения его общего решения. Приведите примеры.

6. Дайте определение линейного дифференциального уравнения первого порядка. Изложите метод нахождения его общего решения. Приведите пример.

7. Что называется особым решением дифференциального уравнения первого порядка?

8. Сформулируйте теорему о существовании и единственности решения дифференциального уравнения второго порядка.

9. Дайте определение линейного дифференциального уравнения n-го порядка (однородного и неоднородного). Докажите основные свойства частных решений линейного однородного дифференциального уравнения.

10. Дайте определение линейно зависимых и линейно независимых функций и приведите примеры.

11. Докажите теорему об общем решении линейного однородного дифференциального уравнения второго порядка.

12. Выведите формулу для общего решения линейного однородного дифференциального уравнения второго порядка с постоянными коэффициентами в случае действительных различных корней характеристического уравнения. Приведите пример.

13. Выведите формулу для общего решения линейного однородного дифференциального уравнения второго порядка с постоянными коэффициентами в случае равных корней характеристического уравнения. Приведите пример.

14. Выведите формулу для общего решения линейного однородного дифференциального уравнения второго порядка с постоянными коэффициентами в случае комплексных корней характеристического уравнения. Приведите пример.

15. Изложите правило нахождения частного решения линейного дифференциального уравнения второго порядка с постоянными коэффициентами и правой частью вида , где 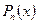— многочлен степени .

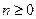16. Изложите правило нахождения частного решения линейного дифференциального уравнения второго порядка с постоянными коэффициентами и правой частью вида 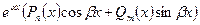, где — многочлены степени m и n соответственно.