Числовые ряды. Определение. Выражение

Определение. Выражение

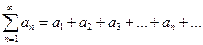(1)

называется рядом, где 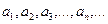– последовательность чисел или функций. Слагаемые 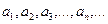– это члены ряда, 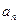– общий член ряда.

Ряд называется числовым, если все его члены являются числами.

Ряд является функциональным, если все члены ряда – функции.

Определение. Сумма конечного числа первых членов ряда называется n-й частичной суммой ряда:

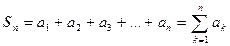. (2)

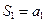— первая частичная сумма,

— вторая частичная сумма,

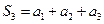— третья частичная сумма,

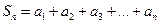— n-я частичная сумма и т.д.

Определение. Если существует конечный предел последовательности частичных сумм

, (3)

то его называют суммой ряда и говорят, что ряд сходится. Если не существует, то говорят, что ряд расходится и суммы не имеет.

Теорема (необходимый признак сходимости ряда).

Если ряд сходится, то предел его общего члена равен нулю при .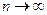

Этот признак не является достаточным, т.е. из того, что 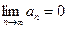, еще не следует, что ряд сходится. Например, 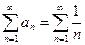– гармонический ряд, 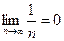, а ряд расходится. Но если 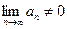, то ряд расходится (это следствие из теоремы), т.е. отличие от нуля 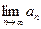является достаточным условием для расходимости ряда .

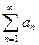Теорема (непредельная форма признака сравнения).

Пусть даны два положительных ряда:

, ,

, .

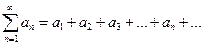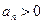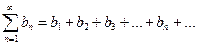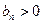Если члены первого ряда не больше соответствующих членов второго ряда и второй ряд сходится, то первый ряд тоже сходится.

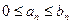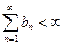Итак, если и , то .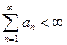

Теорема. Если члены первого ряда не меньше соответствующих членов второго ряда и второй ряд расходится, то первый ряд тоже расходится.

Примечания:

1. Эти две теоремы представляют первый признак сравнения.

2.Часто оказывается полезным рассматривать не соотношение между общими членами a_n, b_n рядов, а предел их отношения 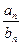при 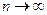, то есть предельную форму первого признака сравнения.

Теорема (второй признак сравнения)

Если для знакоположительных рядов

,

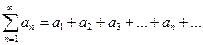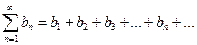
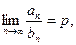
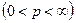, (4)

то эти ряды одновременно сходятся или расходятся.

Следствие. Теорема имеет место, если .