ЛЕКЦИЯ 7 Числовые характеристики случайной величины. Общие сведения

2. Характеристики положения.

3. Моменты. Дисперсия. Среднее квадратическое отклонение.

е) Числовые характеристики случайных величин

Ранее в качестве характеристик случайных величин были рассмотрены:

для дискретной случайной величины:

- функция распределения;

- ряд распределения (графически–многоугольник распределения);

для непрерывной случайной величины:

- функция распределения;

- плотность распределения (графически–кривая распределения).

Каждый закон распределения представляет собой некоторую функцию, и указание этой функции полностью описывает случайную величину с вероятностной точки зрения. Однако во многих случаях нет необходимости определять случайную величину исчерпывающим. образом. Достаточно бывает указать только отдельные числовые параметры, характеризующие основные особенности распределения случайной величины. Пользуясь такими характеристиками, можно выразить все существенные сведения о случайной величине более компактно, с помощью минимального числа параметров. Такие характеристики, назначение которых – выразить в сжатой форме наиболее существенные особенности распределения, называются числовыми характеристиками случайной величины.

Характеристики положения

Среди числовых характеристик случайных величин прежде всего рассмотрим те, которые характеризуют положение случайной величины на числовой оси, т.е. указывают некоторое среднее значение, около которого группируются все возможные значения случайной величина. Среднее значение случайной величины можно рассматривать как некоторое число, являющееся как бы ее представителей и заменяющее ее при грубых ориентировочных расчетах.

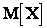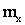Из характеристик положения важнейшую роль играет математическое ожидание случайной величины. Математическое ожидание или является .средневзвешенным значением случайной величины (роль веса каждого значения играет вероятность этого значения) и определяется:

для дискретной величины:

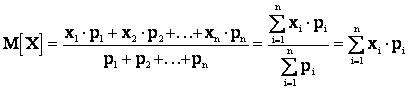, (2.5)

т.к. ;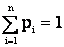

для непрерывной величины:

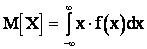(2.6)

Между математическим ожиданием случайной величины 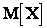и средним арифметическим ее значений 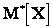та же связь, что между вероятностью события и его частотой. Так, для дискретной величины:

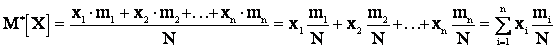
где 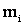– число появлений значения 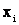случайной величины X;

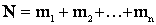– число всех возможных значений X.

Но 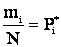есть частота события 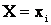, которая при 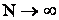стремится к вероятности 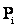, а в этом случае 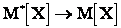, т.е. при увеличении числа опытов ( 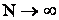) среднее арифметическое значений случайной величины сходится по вероятности к ее математическому ожиданию.

Кроме математического ожидания могут быть использованы и другие характеристики положения – Мода и Медиана случайной величины.

Модой случайной величины (М) называют ее наиболее вероятное значение в случае дискретной величины и значение, в котором плотность вероятности максимальна – в случае непрерывной (рис. 2.7а, 2.7б).

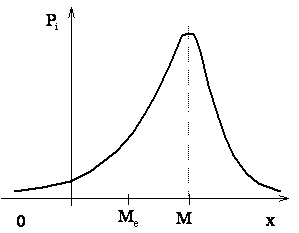
Рис. 2.7а Рис. 2.7б

Если многоугольник распределения (рис. 2.7а) или кривая распределения (рис. 2.7в) имеет один максимум, то распределение называют унимодальным, при нескольких максимумах – полимодальным.

Медианой случайной величины (M_e) называют такое ее значение, для которого:

,

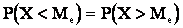т.е. одинаково вероятно, окажется ли случайная величина меньше или больше M_e. Геометрически 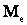есть абсцисса точки, в которой площадь ограниченная кривой распределения делится пополам.

В случае симметричного унимодального распределения медиана, мода и математическое ожидание совпадают.

Моменты. Дисперсия. Среднее квадратическое отклонение.

Кроме характеристик положения, являющихся средними, типичными значениями случайной величины, для ее определения используют ряд характеристик, каждая из которых описывает то или иное свойство распределения. В качестве таких характеристик обычно применяются начальные и центральные моменты.

Начальным моментом s-го порядка называют сумму (для дискретной величины) или интеграл (для непрерывной) следующего вида:

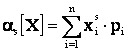(2.7)

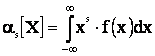(2.8)

Из приведенных соотношений следует, что математическое ожидание есть начальный момент первого порядка ( 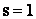) случайной величины X. Пользуясь этим, можно записать:

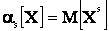(2.9)

т.е. начальный момент s-го порядка случайной величины X есть математическое ожидание s-й степени этой случайной величины.

Для: определения центрального момента необходимо ввести понятие центрированной случайной величины 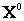, под которой понимают случайную величину, характеризующую отклонение X от ее математического ожидания:

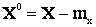
Центральным моментом s-го порядка случайной величины X называется математическое ожидание s-ой степени соответствующей центрированной величины :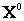

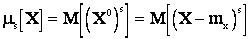. (2.10)

Для дискретной величины:

,

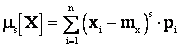для непрерывной величины:

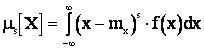
Получим зависимости для вычисления центральных моментов. Центральный момент первого порядка 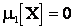, т.к.:

;

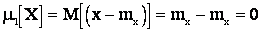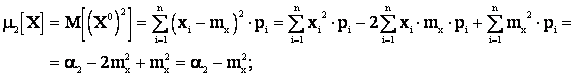
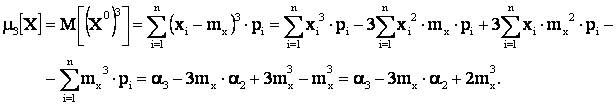
Из всех моментов в качестве характеристик случайной величины чаще всего применяют начальный момент первого порядка 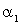, т.е. математическое ожидание и центральный момент второго порядка 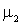, называемый дисперсией.

Дисперсия 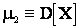есть характеристика рассеивания случайной величины относительно ее математического ожидания. В соответствии с определением для дискретной величины:

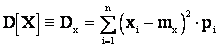, (2.10)

для непрерывной величины:

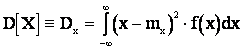. (2.11)

Дисперсия имеет размерность квадрата случайной величины, а для наглядной характеристики рассеивания удобнее пользоваться величиной, размерность которой совпадает с .размерностью случайной величины. Эта величина называется средним квадратическим отклонением (иначе стандартом ) и определяется зависимостью:

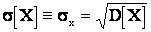(2.12)

Математическое ожидание 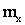, дисперсия 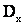или стандарт 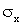– наиболее часто используемые характеристики случайной величины. Они характеризуют наиболее важные черты распределения: его положение и степень разбросанности. Для более подробного описания распределения применяют моменты высших порядков, а именно третий и четвертый центральные моменты.

Третий центральный момент характеризует асимметрию (или скошенность) распределения. Если распределение симметрично относительно математического ожидания, то 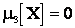. Поскольку 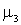имеет размерность куба случайной величины, то для получения безразмерной характеристики асимметрии 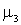делят на 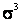. Полученная величина носит название коэффициента асимметрии: .

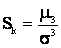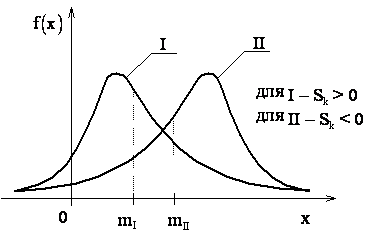
Рис. 2.8.

Четвертый центральный момент характеризует остро или плосковершинность распределения в сравнении о самым распространенным, называемым нормальным. Для нормального распределения 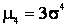, а потому коэффициент, характеризующий островершинность, называемый эскцессом, определяет зависимость: .

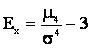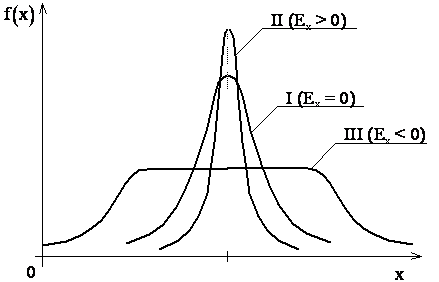
Рис. 2.8.

Для лучшего понимания рассмотренных числовых характеристик полезна аналогия между распределением случайной величины по числовой оси и массы протяженного тела. В соответствии с ней математическому ожиданию аналогична координата центра тяжести; дисперсии – момент инерции тела относительно центра тяжести.

Случайные величины в зависимости от их физического смысла могут иметь различные законы распределения. В теории вероятностей известно большое число таких законов. Однако рассматривать количественные характеристики имеет смысл только для ограниченного их числа. Это объясняется тем, что интересующие исследователя величины (в данном случае это показатели надежности) подчиняются определенным и немногим законам распределения. Такими законами могут быть: экспоненциальный (показательный); Рэлея; нормальный; гамма–распределение; Вейбулла.

Из перечисленных законов особая роль принадлежит нормальному (закону Гаусса).