ЛЕКЦИЯ 6 Функция распределения
2. Вероятность попадания случайной величины на заданный участок.
3. Плотность распределения.
в) Функция распределения
Ряд распределения, давая исчерпывающую характеристику дискретной случайной величине, не может быть использован для задания непрерывной случайной величины.
Для количественной характеристики распределения вероятностей непрерывной величины надо пользоваться не вероятностью события 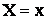 , а вероятностью события
, а вероятностью события 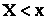 , где x – некоторая текущая переменная. Вероятность этого события зависит от x и есть некоторая функция от x. Эта функция называется функцией распределения случайной величины X и обозначается
, где x – некоторая текущая переменная. Вероятность этого события зависит от x и есть некоторая функция от x. Эта функция называется функцией распределения случайной величины X и обозначается 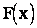 .
.
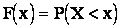 . (2.1)
. (2.1)
Функцию распределения называют также интегральной функцией или интегральным законом распределения .
Функция распределения – самая универсальная характеристика случайной величины. Она существует для всех случайных величин – дискретных и непрерывных, являясь одной из форм закона распределения.
При использовании функции распределения необходимо знание ее общих свойств, к числу которых относятся следующие:
1. Функция распределения есть неубывающая функция своего аргумента, т.е. при 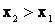
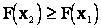 .
.
2. Функция распределения на 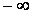 равна 0, т.е.
равна 0, т.е. 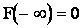 .
.
3. Функция распределения на 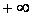 равна 1, т.е.
равна 1, т.е. 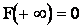 .
.
Эти свойства легко проиллюстрировать используя геометрическую интерпретацию вероятности, рассматривая случайную величину X как случайную точку X на оси 0x. Тогда функция распределения 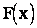 есть вероятность того, что случайная точка X в результате опыта попадет левее точки x (рис. 2.2).
есть вероятность того, что случайная точка X в результате опыта попадет левее точки x (рис. 2.2).
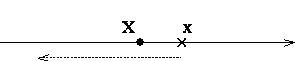
Рис. 2.2.
График функции распределения 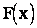 есть график неубывающей функции, значения которой изменяются от 0 до 1, а в некоторых точках функция может претерпевать разрывы. Функция распределения существует как отмечалось и для дискретной случайной величины. Ее легко построить имея ряд распределения.
есть график неубывающей функции, значения которой изменяются от 0 до 1, а в некоторых точках функция может претерпевать разрывы. Функция распределения существует как отмечалось и для дискретной случайной величины. Ее легко построить имея ряд распределения.
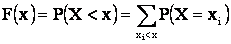 ,
,
где суммирование распространяется лишь на те значения 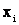 , которые меньше x. Когда текущая переменная проходит через какое-нибудь из возможных значений дискретной величины Х, функция распределения меняется скачкообразно, причем величина скачка равна вероятности этого значения.
, которые меньше x. Когда текущая переменная проходит через какое-нибудь из возможных значений дискретной величины Х, функция распределения меняется скачкообразно, причем величина скачка равна вероятности этого значения.
Так например, пусть закон распределения дискретной случайной величины задан рядом распределения:

Построим график соответствующей функции распределения.
В соответствии с определением:
1) при 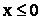
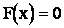
2) при 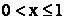
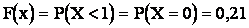 ;
;
3) при 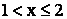
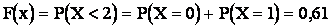 ;
;
4) при 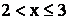
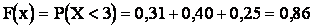 ;
;
5) при 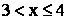
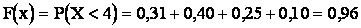 ;
;
6) при 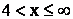
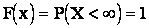 ;
;
График функции распределения представлен на рис. 2.3.
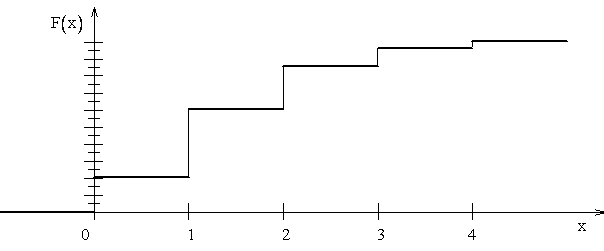
Рис. 2.3
Функция распределения любой дискретной случайной величины есть разрывная функция ступенчатая функция, скачки которой происходят в точках, соответствующих возможным значениям случайной величины и равны вероятностям этих значений. Сумма всех скачков функции 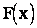 равна 1.
равна 1.
По мере увеличения числа возможных значений случайной величины и уменьшения интервалов между ними число скачков становится больше, а сами скачки – меньше. Ступенчатая кривая становится более плавной (рис. 2.4). Случайная величина постепенно приближается к непрерывной величине, а ее функция распределения – к непрерывной функции (рис. 2.5).
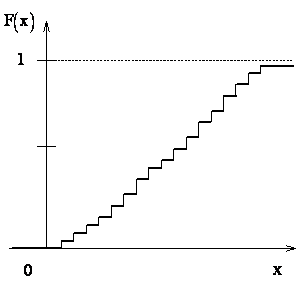
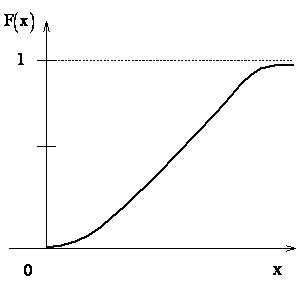
Рис. 2.4 Рис. 2.5
Обычно функция распределения непрерывной случайной величины представляет собой функцию, непрерывную во всех точках (рис. 2.5). Однако можно найти пример случайных величин, возможные значения которых непрерывно заполняют некоторый промежуток, но для которых функция распределения не везде непрерывна, а в отдельных точках терпит разрывы (рис. 2.5а). Такие случайные величины называются смешанными .
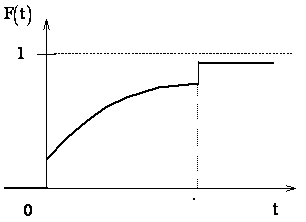
Рис. 2.5а
Пример смешанной величины – время работы до отказа прибора (Т), испытываемого в течении времени 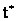 . Функция распределения этой случайной величины непрерывна всюду, кроме точки
. Функция распределения этой случайной величины непрерывна всюду, кроме точки 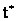 .
.
г) Вероятность попадания случайной величины на заданный участок.
Знание закона распределения случайной величины в форме функции распределения позволяет легко решить важную практическую задачу, а именно: вычислить вероятность того, что случайная величина примет значение, заключенное в некоторых пределах, например от a до b. Это событие определяют термином "попадание случайной величины на участок от a до b".
Условимся для определенности включать в участок 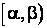 левый конец и не включать правый. Тогда попадание случайной величины Х на участок
левый конец и не включать правый. Тогда попадание случайной величины Х на участок 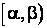 равносильно выполнению неравенства:
равносильно выполнению неравенства:
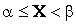 .
.
Вероятность этого события можно выразить через функцию распределения величины X. Для этого рассмотрим три события:
1. Событие А, состоящее в том, что 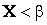 .
.
2. Событие В, состоящее в том, что 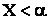 .
.
3. Событие С, состоящее в том, что 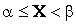 .
.
Учитывая, что 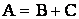 , по теореме сложения вероятностей имеем:
, по теореме сложения вероятностей имеем:
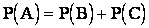 или
или 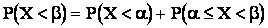 ,
,
откуда
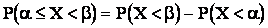 или
или 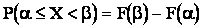 , (2.2)
, (2.2)
т.е. вероятность попадания случайной функции на заданный участок равна приращению функции распределения на этом участке.
Полученная зависимость позволяет определить вероятность принятия случайной величиной любого отдельного значения на участке 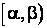 . Будем неограниченно уменьшать участок, полагая, что
. Будем неограниченно уменьшать участок, полагая, что 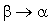 . Тогда из (2.2) следует:
. Тогда из (2.2) следует:
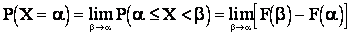 . (*)
. (*)
Значение этого предела зависит от того, непрерывна ли функция 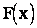 в точке
в точке 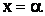 или же терпит разрыв. Если
или же терпит разрыв. Если 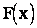 в точке
в точке 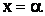 терпит разрыв, то предел (*) равен значению скачка
терпит разрыв, то предел (*) равен значению скачка 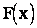 в точке
в точке 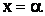 . Если же функция
. Если же функция 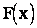 в точке
в точке 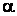 непрерывна, то предел (*) равен 0. Таким образом, вероятность любого отдельного значения непрерывной случайной величины равна 0.
непрерывна, то предел (*) равен 0. Таким образом, вероятность любого отдельного значения непрерывной случайной величины равна 0.
Из того, что событие 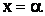 имеет вероятность, равную нулю, не следует, что это событие не будет появляться, т.е. что частота этого события равна 0. Частота события даже при большом числе опытов не равна, а лишь приближается к вероятности. Из того, что вероятность события
имеет вероятность, равную нулю, не следует, что это событие не будет появляться, т.е. что частота этого события равна 0. Частота события даже при большом числе опытов не равна, а лишь приближается к вероятности. Из того, что вероятность события 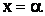 равна нулю, следует только то, что при неограниченном повторении опыта это событие будет появляться сколь угодно редко.
равна нулю, следует только то, что при неограниченном повторении опыта это событие будет появляться сколь угодно редко.
д) Плотность распределения.
Функция распределения, увеличиваясь от значения к значению, является функцией "накопленной" вероятности и не дает простого и наглядного представления о законе распределения случайной величины. Этого недостатка лишена функция 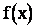 , называемая плотностью распределения или плотностью вероятности , или дифференциальной функцией распределения случайной величины X.
, называемая плотностью распределения или плотностью вероятности , или дифференциальной функцией распределения случайной величины X.
Для получения ее рассмотрим вероятность попадания случайной величины X на участок 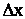 :
:
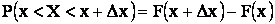
Найдем теперь среднюю вероятность, приходящуюся на единицу длины этого участка, а сам участок будет стягивать в точку за счет 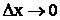 :
:
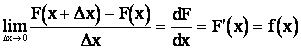 . (2.3)
. (2.3)
Функция 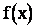 – производная функции распределения характеризует как бы плотность, с которой распределяются значения случайной величины в данной точке. График
– производная функции распределения характеризует как бы плотность, с которой распределяются значения случайной величины в данной точке. График 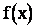 называют кривой распределения (рис. 2.6).
называют кривой распределения (рис. 2.6).

Рис. 2.6
Плотность распределения как и функция распределения есть одна из форм задания закона распределения. Эта форма более удобна и наглядна, однако она существует только для непрерывных случайных величин.
С помощью плотности распределения легко вычислить вероятность попадания случайной величины на заданный участок. Если это элементарный участок 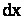 , то искомая вероятность равна
, то искомая вероятность равна 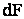 и в соответствии с (2.3) равна
и в соответствии с (2.3) равна 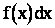 . Величина
. Величина 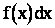 называется элементом вероятности и имеет определенную геометрическую интерпретацию (рис. 2.6). Вероятность попадания случайной величины на конечный участок
называется элементом вероятности и имеет определенную геометрическую интерпретацию (рис. 2.6). Вероятность попадания случайной величины на конечный участок 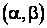 равна интегралу от элемента вероятности:
равна интегралу от элемента вероятности:
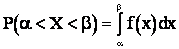 . (2.4)
. (2.4)
Включение или исключение из интервала конечных значений a и b роли не играют, т.к.
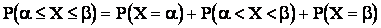 ,
,
но для непрерывной случайной величины:
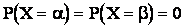 ,
,
тогда:
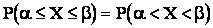 .
.
По плотности распределения легко найти функцию распределения:J–
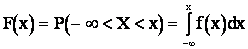 .
.
Отметим основные свойства плотности распределения.
1. Плотность распределения есть неотрицательная функция:
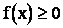
т.к. 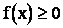 – неубывающая функция.
– неубывающая функция.
2. Интеграл в бесконечных пределах от плотности распределения равен 1.
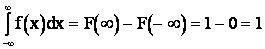 .
.
Геометрически основные свойства плотности распределения означают, что:
¾ во-первых вся кривая распределения лежит не ниже оси абсцисс;
¾ во-вторых полная площадь, ограниченная кривой распределения и осью абсцисс, равна единице.
Дата добавления: 2014-12-03; просмотров: 2812;
