ЛЕКЦИЯ 11 Постановка задачи по нахождению параметров распределения
2. Оценки для математического ожидания и дисперсии.
3. Доверительный интервал, доверительная вероятность.
г) Нахождение неизвестных параметров распределения.
Для определения закона распределения необходимо располагать обширным статистическим материалом. На практике приходится иметь дело с материалом ограниченного объема – несколько десятков наблюдений. На основе ограниченного статистического материала можно определить основные числовые характеристики случайной величины, – и это – важнейшая задача математической статистики.
Необходимо отметить, что любое значение искомого параметра, вычисленное на основе ограниченного числа опытов, всегда содержит элемент случайности. Такое приближенное, случайное значение называют оценкой параметра. Любая из таких оценок случайна. При пользовании ею неизбежны ошибки. Желательно выбрать такую оценку, чтобы эти ошибки были по возможности минимальны.
Выясним, каким требованиям должна в таком случае удовлетворять оценка. Рассмотрим случайную величину X, закон распределения которой содержит неизвестный параметр a. Найдем оценку для параметра а по результатам n независимых опытов. В каждом опыте величина X принимала определенное значение, которое обозначим как 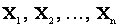 . Будем рассматривать их как n независимых случайных величин. Такое рассмотрение правомерно, так как выбор n опытов из ограниченного материала произволен и результат 1-го, 2-го. ... n-го из них, т.е.
. Будем рассматривать их как n независимых случайных величин. Такое рассмотрение правомерно, так как выбор n опытов из ограниченного материала произволен и результат 1-го, 2-го. ... n-го из них, т.е. 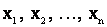 ; можно считать реализацией соответствующей случайной величины
; можно считать реализацией соответствующей случайной величины 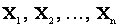 .
.
Обозначим оценку параметра а через 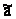 . Она представляет собой функцию случайных величин
. Она представляет собой функцию случайных величин 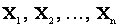 , т.е.:
, т.е.:
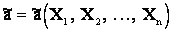 ,
,
а потому сама является случайной величиной. Закон распределения 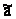 определяется законом распределения величины Х и числом опытов n.
определяется законом распределения величины Х и числом опытов n.
Оценка 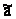 должна удовлетворять ряду требований, важнейшими из которых являются три следующих:
должна удовлетворять ряду требований, важнейшими из которых являются три следующих:
1. При увеличении числа опытов n оценка должна сходиться к оцениваемому параметру. Оценка, обладающая таким свойством называется состоятельной .
2. Использование оценки 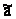 вместо параметра а не должно приводить к систематической ошибке в сторону завышения или занижения, т.е. необходимо, чтобы выполнялось условие
вместо параметра а не должно приводить к систематической ошибке в сторону завышения или занижения, т.е. необходимо, чтобы выполнялось условие 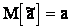 . Оценка, удовлетворяющая этому условию называется несмещенной .
. Оценка, удовлетворяющая этому условию называется несмещенной .
3. Несмещенная оценка должна обладать в сравнении с другими наименьшей дисперсией, т.е.
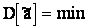 .
.
Оценка, обладающая этим свойством называется эффективной .
На практике всем этим требованиям удается удовлетворить не всегда.
Оценка для математического ожидания и дисперсии
Имеется случайная величина Х с математическим ожиданием m и дисперсией D; оба параметра неизвестны. Над величиной Х произведено n независимых опытов, давших результаты: 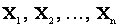 . Необходимо найти оценки для параметров m и D.
. Необходимо найти оценки для параметров m и D.
Имеющийся материал о случайной величине Х следует рассматривать как первичный статистический или выборочный. Числовыми характеристиками распределения, построенного по этому материалу являются (как указывалось в 2.1.36) выборочное среднее 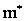 и выборочная дисперсия
и выборочная дисперсия 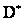 . Выясним возможность их использования в качестве оценок параметров m и D.
. Выясним возможность их использования в качестве оценок параметров m и D.
Оценка для математического ожидания.
В качестве оценки используем выборочное среднее 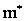 :
:
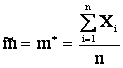 ,
,
(запись 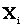 вместо
вместо 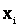 подчеркивает случайность получаемого результата, вероятность которого
подчеркивает случайность получаемого результата, вероятность которого 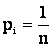 ).
).
Предлагаемая оценка является:
1. Состоятельной, т.к. при 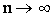
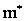 по вероятности сходится к m.
по вероятности сходится к m.
2. Несмещенной, т.к.:
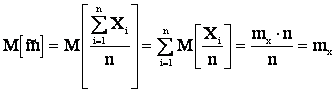 .
.
3. Эффективной, т.к.:
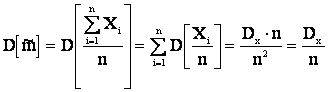 .
.
Если величина X распределена по нормальному закону, то 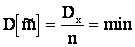 , а для других распределений – близка к минимуму.
, а для других распределений – близка к минимуму.
Оценка для дисперсии.
В качестве оценки используем выборочную дисперсию 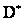 :
:
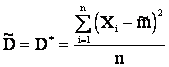 .
.
1. Проверка состоятельности.
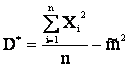 , но
, но 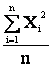 сходится по вероятности к
сходится по вероятности к 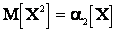 , а
, а 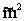 сходится по вероятности к
сходится по вероятности к 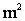 . Тогда
. Тогда 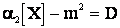 , а следовательно оценка
, а следовательно оценка
2. Проверка несмещенности.
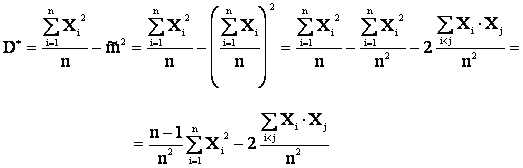
Математическое ожидание выборочной дисперсии определяется:
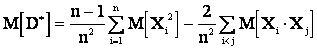 .
.
Дисперсия не зависит от выбора начала координат. Выберем его в точке m. Тогда 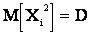 ;
; 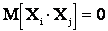 . В результате
. В результате 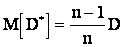 . Таким образом, оценка
. Таким образом, оценка 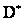 не является несмещенной. В качестве оценки для D следует выбрать скорректированную статистическую дисперсию
не является несмещенной. В качестве оценки для D следует выбрать скорректированную статистическую дисперсию 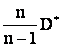 , тогда
, тогда  . Предложенная оценка является несмещенной, что нетрудно показать.
. Предложенная оценка является несмещенной, что нетрудно показать.
В результате: если имеется ограниченный статистический материал, содержащий значения 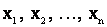 , принятые в n независимых опытах случайной величинах Х с неизвестными математическим ожиданием m и дисперсией D, то для определения этих параметров используются зависимости:
, принятые в n независимых опытах случайной величинах Х с неизвестными математическим ожиданием m и дисперсией D, то для определения этих параметров используются зависимости:
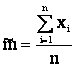 , (2.26)
, (2.26)
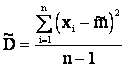 . (2.27)
. (2.27)
Доверительный интервал. Доверительная вероятность.
Ранее был рассмотрен вопрос об оценке неизвестного параметра а. Причем оценка была дана в виде некоторого значения 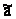 . Эта оценка называется точечной. В большинстве задач требуется не только найти для параметра а подходящее численное значение, но и оценить его точность и надежность.
. Эта оценка называется точечной. В большинстве задач требуется не только найти для параметра а подходящее численное значение, но и оценить его точность и надежность.
Чтобы дать представление о точности и надежности оценки 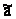 , используются так называемые доверительные интервалы и доверительные вероятности.
, используются так называемые доверительные интервалы и доверительные вероятности.
Пусть для параметра а получена из опыта несмещенная оценка 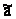 . Оценим возможную при этом ошибку. Назначим некоторую достаточно большую вероятность b (например
. Оценим возможную при этом ошибку. Назначим некоторую достаточно большую вероятность b (например 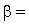 0,9; 0,95 или 0,99) такую, что событие с вероятностью b можно считать практически достоверным и найдем такое значение e, для которого:
0,9; 0,95 или 0,99) такую, что событие с вероятностью b можно считать практически достоверным и найдем такое значение e, для которого:
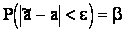 . (*)
. (*)
Тогда диапазон практически возможных значений ошибки, возникающей при замене а на 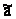 будет
будет 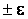 . Большие по абсолютной величине ошибки будут появляться лишь с малой вероятностью
. Большие по абсолютной величине ошибки будут появляться лишь с малой вероятностью 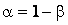 . Зависимость (*) можно записать в виде:
. Зависимость (*) можно записать в виде:
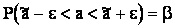 . (**)
. (**)
Равенство (**) означает, что с вероятностью b неизвестное значение параметра а попадает в интервал 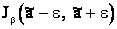 . В данном случае величина а не случайна, но случаен интервал
. В данном случае величина а не случайна, но случаен интервал 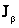 . Случайно его положение на оси абсцисс, определяемое его центром
. Случайно его положение на оси абсцисс, определяемое его центром 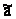 , случайна и длина интервала
, случайна и длина интервала 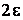 , т.к. величина e вычисляется как правило по опытным данным. Поэтому b следует толковать не как вероятность попадания точки а в интервал
, т.к. величина e вычисляется как правило по опытным данным. Поэтому b следует толковать не как вероятность попадания точки а в интервал 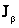 , а как вероятность того, что случайный интервал
, а как вероятность того, что случайный интервал 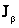 накроет а. Вероятность b называют доверительной вероятностью , а интервал
накроет а. Вероятность b называют доверительной вероятностью , а интервал 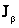 – доверительным интервалом . Границы интервала
– доверительным интервалом . Границы интервала 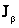 :
: 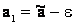 ,
, 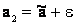 называются доверительными границами (рис. 2.16).
называются доверительными границами (рис. 2.16).

Рис. 2.16
Определим доверительные границы. Пусть для параметра а имеется несмещенная оценка 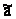 . Если бы закон распределения
. Если бы закон распределения 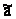 был известен, то доверительные границы определились решением уравнения:
был известен, то доверительные границы определились решением уравнения:
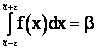 .
.
Но закон распределения оценки 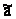 зависит от закона распределения самой величины X, а следовательно от его неизвестных параметров, в том числе и от самого параметра a.
зависит от закона распределения самой величины X, а следовательно от его неизвестных параметров, в том числе и от самого параметра a.
Чтобы обойти это затруднение при нахождении доверительных границ вместо параметров закона распределения оценки 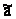 приходится использовать их точечные оценки. При сравнительно большом числе опытов
приходится использовать их точечные оценки. При сравнительно большом числе опытов 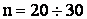 этот прием дает сравнительно неплохой результат.
этот прием дает сравнительно неплохой результат.
В качестве примера рассмотрим задачу о доверительном интервале для математического ожидания.
Пусть произведено n независимых опытов над случайной величиной X, характеристики которой – математическое ожидание m и дисперсия D – неизвестны.
Для этих параметров получены оценки, и в частности для математического ожидания 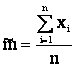 .
.
Требуется построить доверительный интервал 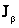 , соответствующий доверительной вероятности b для математического ожидания m величины X.
, соответствующий доверительной вероятности b для математического ожидания m величины X.
При решении этой задачи воспользуемся тем, что величина 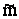 представляет собой сумму n независимых одинаково распределенных случайных величин
представляет собой сумму n независимых одинаково распределенных случайных величин 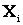 при достаточно большом n, а потому закон ее распределения будет близок к нормальному. Т.о. можно считать, что величина
при достаточно большом n, а потому закон ее распределения будет близок к нормальному. Т.о. можно считать, что величина 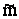 распределена по нормальному закону, характеристики, которого соответственно равны m и
распределена по нормальному закону, характеристики, которого соответственно равны m и 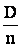 . Тогда:
. Тогда:
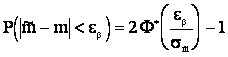
Для определения 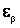 необходимо решить уравнение:
необходимо решить уравнение:
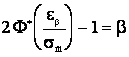 или
или 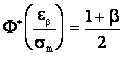 .
.
Его решение 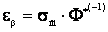 , где
, где 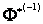 – функция обратная
– функция обратная 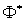 , ее удобно получить с помощью таблиц обратных функций
, ее удобно получить с помощью таблиц обратных функций 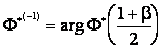 Отсюда зная
Отсюда зная 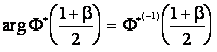 и
и 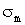 (здесь приходится использовать ее точечную оценку
(здесь приходится использовать ее точечную оценку 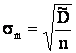 ), определяется
), определяется 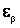 :
:
Дата добавления: 2014-12-03; просмотров: 1234;
