ЛЕКЦИЯ 12 Предмет теории массового обслуживания
2. Случайный процесс со счетным множеством состояний.
3. Поток событий.
2.2. Элементы теории массового обслуживания. 2.2.1. Предмет теории массового обслуживания. В последнее время, в самых разных областях практики возникла необходимость в решении своеобразных вероятностных задач, связанных с работой так называемых систем массового обслуживания. Примерами таких систем могут служить: ремонтные мастерские, автозаправочные станции, справочные бюро и т.п. Характерной чертой каждой такой системы является наличие определенного числа обслуживающих единиц, называемых "каналами обслуживания". В качестве каналов могут фигурировать: линии связи, лица выполняющие те или иные операции, различные приборы и т.п.
Задачи, решаемые методами теории массового обслуживания возникают в связи с проблемой организации транспорта и систем сообщений. Этими же методами пользуются при решении задач, относящихся к надежности технических устройств и, в частности, при определении таких характеристик как среднего времени простоя в связи с ремонтом, потребного количества запасных деталей и т.д.
Работа любой системы массового обслуживания состоит в выполнении поступающего на нее потока требований или заявок. Заявки поступают одна за другой в некоторые, как правило, случайные моменты времени. Обслуживание поступившей заявки продолжается определенное время, после чего канал освобождается и снова готов для приема следующей. Каждая система массового обслуживания, в зависимости от числа каналов и их производительности, обладает какой-то пропускной способностью, позволяющей ей более или менее успешно справляться с потоком заявок.
Предмет теории массового обслуживания – установление зависимости между характером потока заявок, производительностью отдельного канала, числом каналов и эффективностью обслуживания. В качестве характеристик эффективности могут быть использованы различные показатели например: средний процент заявок, получающих отказ и покидающих систему необслуженными; среднее время простоя отдельных каналов и системы в целом; вероятность принятия поступившей заявки к немедленному обслуживанию и т.п. Каждая из этих характеристик описывает с той или другой стороны, степень приспособленности системы к выполнению потока заявок, т.е. ее пропускную способность.
Под пропускной способностью понимают среднее число заявок, которое система может обслужить в единицу времени. Пропускная способность зависит не только от параметров системы, но и от характера потока заявок. Обычно моменты поступления заявок случайны; по большей части случайна и длительность обслуживания заявки. Таким образом, процесс функционирования системы массового обслуживания представляет собой случайный процесс. Рассмотрим его.
2.2.2. Случайный процесс со счетным множеством состояний. Случайный процесс, протекающий в системе массового обслуживания состоит в том, что система в случайные моменты времени переходит из одного состояния в другое: меняется число занятых каналов, число заявок в очереди и т.п. Количество таких состояний конечно (или счетно), а переход из одного состояния в другое осуществляется мгновенным скачком, в момент, когда осуществляется соответствующее событие.
Рассмотрим физическую систему X со счетным множеством состояний 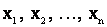 . В любой момент времени t система X может быть в одном из этих состояний. Обозначим
. В любой момент времени t система X может быть в одном из этих состояний. Обозначим 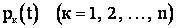 вероятность того, что в момент t система будет находиться в состоянии
вероятность того, что в момент t система будет находиться в состоянии 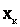 .
.
Совокупность вероятностей 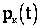 для каждого момента времени t характеризует данное сечение случайного процесса. Эта совокупность достаточно хорошо описывает процесс и для большинства практических применений оказывается достаточной.
для каждого момента времени t характеризует данное сечение случайного процесса. Эта совокупность достаточно хорошо описывает процесс и для большинства практических применений оказывается достаточной.
Для изучения случайных процессов со счетным множеством состояний используются специальные схемы – графы состояний. На них условно изображают возможные состояния системы в различные моменты времени и возможные переходы между ними. Например, граф состояний одноканальной системы с четырьмя следующими состояниями:
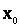 – канал исправен и свободен;
– канал исправен и свободен;
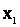 – канал исправен и занят;
– канал исправен и занят;
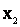 – канал неисправен и ждет ремонта;
– канал неисправен и ждет ремонта;
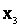 – канал неисправен и ремонтируется;
– канал неисправен и ремонтируется;
имеет вид, приведенный на рис. 2.17.
Для описания случайного процесса, протекающего в рассматриваемой системе, т.е. определения совокупностей 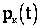 , необходимо проанализировать причины, вызывающие переход системы из состояния в состояние. Для системы массового обслуживания основным фактором, обусловливающим протекающие в ней процессы, является поток заявок. Поэтому математическое описание любой системы массового обслуживания начинают с описания потока заявок (событий).
, необходимо проанализировать причины, вызывающие переход системы из состояния в состояние. Для системы массового обслуживания основным фактором, обусловливающим протекающие в ней процессы, является поток заявок. Поэтому математическое описание любой системы массового обслуживания начинают с описания потока заявок (событий).

Рис. 2.17
2.2.3. Поток событий Под потоком событий в теории вероятностей начинается последовательность событий, происходящих одно за другим в какие-то моменты времени. Примерами могут служить: поток включения приборов в бытовой электросети, поток сбоев ЭВМ и т.п. События, образующие поток, в общем случае могут быть различными, но здесь будет рассмотрен лишь поток однородных событий, отличающихся только моментами появления. Такой поток можно изобразить как последовательность точек 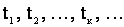 на числовой оси (рис. 2.18), соответствующих моментам появления событий.
на числовой оси (рис. 2.18), соответствующих моментам появления событий.

Рис. 2.18
Поток событий называется регулярным, если события следуют одно за другим через строго определенные промежутки времени. Это – предельный случай, практически не встречающийся в реальных ситуациях. Типичным для системы массового обслуживания является случайный поток заявок (событий).
В связи с простотой описания и возможностью широкого применения будем рассматривать поток, называемый простейшим или стационарным пуассоновским. Этот поток событий должен удовлетворять трем требованиям:
1. Быть стационарным . Это значит, что вероятность попадания того или иного числа событий на участок времени длиной t зависит только от длины участка и не зависит от расположения его на оси 0t.
2. Не иметь последействия . Это значит, что для любых неперекрывающихся участков времени число событий, попадающих на один из них, не зависит от числа событий, попадающих на другие.
3. Быть ординарным . Это значит, что вероятность попадания на участок 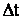 двух или более событий пренебрежительно мала по сравнению с вероятностью попадания одного события.
двух или более событий пренебрежительно мала по сравнению с вероятностью попадания одного события.
Простейший поток играет среди потоков событий особую роль, в определенной мере аналогичную роли нормального закона среди других законов распределения. При взаимном наложении большого числа (4,5 и более) ординарных, стационарных потоков с практически любым последействием получается поток, сколь угодно близкий к простейшему. Необходимо лишь, чтобы складываемые потоки оказывали на результирующий приблизительно равномерно малое влияние. Важность простейшего потока в теории массового обслуживания очевидна. Во-первых, простейшие и близкие к простейшим потоки заявок часто встречаются на практике; во-вторых, любой поток заявок (с определенной погрешностью) может быть заменен простейшим с той же плотностью. Поэтому рассмотрим более подробно этот поток и его свойства.
Представим простейший поток как неограниченную последовательность случайных точек (рис. 2.18). Выделим произвольный участок времени длиною t. Можно доказать, что вероятность того, что за время t произойдет ровно m событий равна:
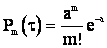 , (2.28)
, (2.28)
где а – математическое ожидание числа событий за время t.
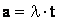 ,
,
где 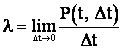 – параметр или интенсивность потока событий;
– параметр или интенсивность потока событий;
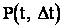 – вероятность появления события на интервале
– вероятность появления события на интервале 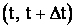 .
.
Зависимость (2.28) определяет закон распределения Пуассона. Многоугольники распределения случайной величины, распределенной по этому закону, представлены на рис. 2.19.
Важной характеристикой потока является закон распределения длины промежутка между соседними событиями (Т).
Функция распределения для этой случайной величины Т запишется:
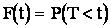 .
.
Вероятность противоположного события и состоящего в том, что на участке времени длиною t, начинающемуся в момент 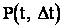 , не появится ни одного из последующих событий составит:
, не появится ни одного из последующих событий составит:
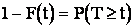

Рис. 2.19
Но вероятность того, что участок времени t будет пустым, т.е. 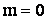 , можно найти по (2.28):
, можно найти по (2.28):
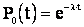 , откуда:
, откуда:
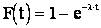 . (2.29)
. (2.29)
Дифференцируя (2.29), найдем плотность распределения случайной величины Т:
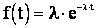 . (2.30)
. (2.30)
Закон распределения с плотностью определенной по (2.30) называется показательным, а величина l – его параметром. График плотности 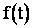 представлен на рис. 2.20.
представлен на рис. 2.20.
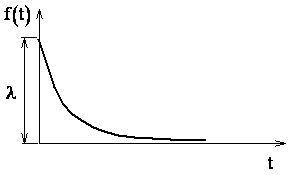
Рис. 2.20
Математическое ожидание и дисперсия случайной величины, распределенной по показательному закону определяется:
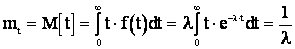 ; (2.31)
; (2.31)
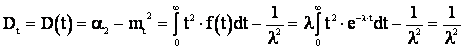 ; (2.32)
; (2.32)
откуда:
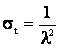 .
.
Показательный закон обладает замечательным свойством, состоящим в следующем: если промежуток времени, распределенный по показательному закону уже длился некоторое время t, то это никак не влияет на закон распределения оставшейся части промежутка: он будет таким же, как и закон распределения всего промежутка Т. Таким образом, если промежуток Т распределен по показательному закону, то любые сведения о том, сколько времени уже протекал этот промежуток, не влияют на закон распределения оставшегося времени.
Дата добавления: 2014-12-03; просмотров: 1279;
