ЛЕКЦИЯ 10 Постановка задачи по проверке правдоподобия гипотез
2. Критерий Пирсона.
3. Методика применения критерия Пирсона.
в). Проверка правдоподобия гипотез
Пусть данное статистическое распределение выровнено с помощью некоторой теоретической кривой 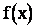 . Как бы хорошо ни была подобрана теоретическая кривая между ней и статистическим распределением неизбежны расхождения. Они могут быть несущественными и объясняться случайными обстоятельствами, связанными с ограниченным числом наблюдений, а могут быть существенными и объясняться тем, что подобранная теоретическая кривая не соответствует данному статистическому распределению. Для ответа на вопрос какой именно случай имеет место, а следовательно, можно или нельзя принять предложенную гипотезу о законе распределения, используются так называемые критерии согласия .
. Как бы хорошо ни была подобрана теоретическая кривая между ней и статистическим распределением неизбежны расхождения. Они могут быть несущественными и объясняться случайными обстоятельствами, связанными с ограниченным числом наблюдений, а могут быть существенными и объясняться тем, что подобранная теоретическая кривая не соответствует данному статистическому распределению. Для ответа на вопрос какой именно случай имеет место, а следовательно, можно или нельзя принять предложенную гипотезу о законе распределения, используются так называемые критерии согласия .
Поясним их применение. Пусть на основании имеющегося статистического материала необходимо проверить гипотезу H, состоящую в том. что случайная величина Х подчиняется определенному закону распределения, заданному, например, в виде функции распределения 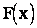 .
.
Для того, чтобы принять или отвергнуть гипотезу Н, рассмотрим некоторую величину U, характеризующую степень расхождения теоретического и статистического распределений. Величина U может быть выбрана различными способами, например, в качестве U можно взять сумму квадратов отклонений теоретических вероятностей 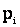 от соответствующих частот
от соответствующих частот 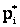 или же максимальное отклонение статистической функции распределения
или же максимальное отклонение статистической функции распределения 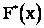 от теоретической
от теоретической 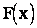 и т.д. Величина U – случайная величина и закон ее распределения зависит от закона распределения случайной величины Х и от числа опытов n. Если гипотеза Н верна, то закон распределения величины U определяется законом распределения величины Х (т.е. функцией
и т.д. Величина U – случайная величина и закон ее распределения зависит от закона распределения случайной величины Х и от числа опытов n. Если гипотеза Н верна, то закон распределения величины U определяется законом распределения величины Х (т.е. функцией 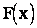 и числом n).
и числом n).
Допустим, что этот закон известен. В результате серии опытов обнаружено, что выбранная мера расхождения U приняла некоторое значение u. Можно ли объяснить это случайными причинами или же следует отметить, что расхождение слишком велико и указывает на наличие существенной разницы между теоретическим и статистическим распределением, а следовательно на непригодность гипотезы Н? Для ответа на этот вопрос предположим, что гипотеза Н верна, и вычислим при этом предположении вероятность того, что за счет случайных причин , связанных с недостаточным объемом опытного материала, мера расхождения окажется не меньше, чем определенное в опыте значение u, т.е. вычислим вероятность события 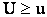 . Если эта вероятность мала, то гипотезу Н следует отвергнуть как малопригодную; если же эта вероятность значительна, то следует признать, что экспериментальные данные не противоречат гипотезе Н.
. Если эта вероятность мала, то гипотезу Н следует отвергнуть как малопригодную; если же эта вероятность значительна, то следует признать, что экспериментальные данные не противоречат гипотезе Н.
Остановимся теперь на выборе меры расхождения U. Установлено, что при определенных способах ее выбора. закон распределения величины U обладает простыми свойствами и при достаточно большом n практически не зависит от функции 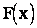 . Именно такими мерами расхождения пользуются в математической статистике в качестве критериев согласия.
. Именно такими мерами расхождения пользуются в математической статистике в качестве критериев согласия.
Рассмотрим один из наиболее часто применяемых критериев согласия – критерий Пирсона или критерий 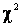 .
.
Пусть результаты n независимых опытов над случайной величиной Х оформлены в виде статистического ряда.

Проверим, согласуются ли экспериментальные данные с гипотезой о том, что случайная величина Х имеет закон распределения, заданный функцией 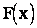 .
.
Зная этот закон, можно найти теоретические вероятности попадания случайной величины в каждый из разрядов:
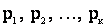 .
.
Проверка согласованности теоретического и статистического распределений проводится, исходя из расхождений между теоретическими вероятностями 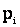 и наблюденными частотами
и наблюденными частотами 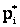 . В качестве меры расхождения выбирается сумма квадратов отклонений
. В качестве меры расхождения выбирается сумма квадратов отклонений 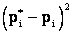 , взятых с некоторыми "весами"
, взятых с некоторыми "весами" 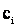 :
:
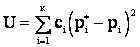 (2.24)
(2.24)
Веса разрядов 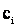 вводятся потому, что отклонения относящиеся к различным разрядам нельзя считать равноправными по значимости: отклонение
вводятся потому, что отклонения относящиеся к различным разрядам нельзя считать равноправными по значимости: отклонение 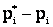 может быть мало значимым, если сама вероятность
может быть мало значимым, если сама вероятность 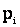 велика, и очень существенным, если она мала. Поэтому
велика, и очень существенным, если она мала. Поэтому 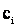 выбирают обратно пропорциональными вероятностям разрядов
выбирают обратно пропорциональными вероятностям разрядов 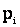 .
.
Пирсон показал, что если положить
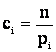
то при больших n закон распределения величины U обладает простыми свойствами, а именно: он практически не зависит от функции распределения 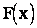 и от числа опытов n, а зависит только от числа разрядов к.
и от числа опытов n, а зависит только от числа разрядов к.
При таком выборе коэффициентов 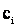 , мера расхождения обозначается
, мера расхождения обозначается 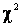 и в соответствии с (2.24) имеет вид:
и в соответствии с (2.24) имеет вид:
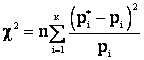 (2.24а)
(2.24а)
Вводя n под знак суммы, и учитывая, что 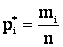 , где
, где 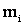 – число значений в i-ом разряде, (2.24а) запишется:
– число значений в i-ом разряде, (2.24а) запишется:
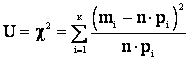
Распределение 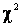 зависит от параметра
зависит от параметра 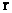 , называемого числом степеней свободы распределения. Число степеней свободы
, называемого числом степеней свободы распределения. Число степеней свободы 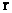 равно числу разрядов к за вычетом числа независимых условий (связей), наложенных на частоты
равно числу разрядов к за вычетом числа независимых условий (связей), наложенных на частоты 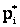 . Примерами таких условий могут быть:
. Примерами таких условий могут быть:
1. 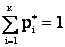
Это требование накладывается всегда.
2. 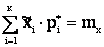
Это условие требует совпадения теоретического и статистического средних значений.
3. 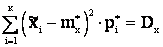
Это условие требует совпадения теоретической и статистической дисперсий.
Для распределения 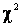 составлены специальные таблицы. Пользуясь ими, можно для каждого значения
составлены специальные таблицы. Пользуясь ими, можно для каждого значения 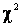 и числа степеней свободы r найти вероятность р того. что величина распределенная по закону
и числа степеней свободы r найти вероятность р того. что величина распределенная по закону 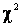 превзойдет это значение.
превзойдет это значение.
Таблица 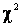

Распределение 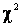 дает возможность оценить степень согласованности теоретического и статистического распределении. Если исходить из того, что величина
дает возможность оценить степень согласованности теоретического и статистического распределении. Если исходить из того, что величина 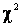 действительно распределена по закону
действительно распределена по закону 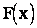 , то вероятность р, определенная по таблице, есть вероятность того, что за счет чисто случайных причин мера расхождения теоретического и статистического распределений (2.25) будет не меньше, чем фактически наблюденное в данной в данной серии опытов значение
, то вероятность р, определенная по таблице, есть вероятность того, что за счет чисто случайных причин мера расхождения теоретического и статистического распределений (2.25) будет не меньше, чем фактически наблюденное в данной в данной серии опытов значение 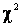 . При малом значение вероятности
. При малом значение вероятности 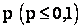 результат опыта следует считать противоречащим гипотезе Н о том, что закон распределения величины Х есть
результат опыта следует считать противоречащим гипотезе Н о том, что закон распределения величины Х есть 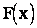 . Эту гипотезу следует отбросить как неправдоподобную. При сравнительно большой вероятности р расхождения между теоретическим и статистическим расхождениями можно считать несущественными и отнести за счет случайных причин . В этом случае гипотезу Н можно считать правдоподобной.
. Эту гипотезу следует отбросить как неправдоподобную. При сравнительно большой вероятности р расхождения между теоретическим и статистическим расхождениями можно считать несущественными и отнести за счет случайных причин . В этом случае гипотезу Н можно считать правдоподобной.
Таким образом, алгоритм использования критерия 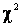 следующий:
следующий:
1. По формуле (2.25) определяется мера расхождения 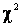 .
.
2. Определяется число степеней свободы 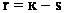 , где s – число наложенных связей.
, где s – число наложенных связей.
3. По r и 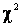 с помощью таблиц определяется вероятность того, что величина имеющая распределение
с помощью таблиц определяется вероятность того, что величина имеющая распределение 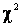 с r степенями свободы превзойдет данное значение
с r степенями свободы превзойдет данное значение 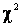 . Если эта вероятность мала, гипотеза отбрасывается как неправдоподобная. Если же вероятность р велика, то этот факт еще нельзя считать доказательством справедливости гипотезы Н; он указывает лишь на то, что гипотеза не противоречит опытным данным.
. Если эта вероятность мала, гипотеза отбрасывается как неправдоподобная. Если же вероятность р велика, то этот факт еще нельзя считать доказательством справедливости гипотезы Н; он указывает лишь на то, что гипотеза не противоречит опытным данным.
Особо следует отметить случай получения очень больших значений вероятности р, например, р = 0,99. Это означает, что с вероятностью 0,99 за счет чисто случайных причин должны получаться расхождения больше, чем наблюденное. Столь близкое совпадение теоретического и статистического распределений (99 случаев из 100 будут давать рассогласование большее, чем наблюденное), не является случайным, а может быть объяснено некорректной регистрацией и обработкой опытных данных (произвольное исключение данных или их изменение).
Дата добавления: 2014-12-03; просмотров: 1196;
